Binomi de Newton

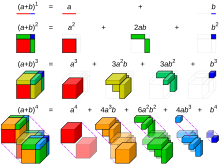
El Binomi de Newton o teorema del binomi és una fórmula que serveix per a calcular la potència $n$ d'un binomi $(a+b)$. És per tant una generalització de les fórmules elementals $(a+b)^{2}=a^{2}+2ab+b^{2}$ i $(a+b)^{3}=a^{3}+3a^{2}b+3ab^{2}+b^{3}$. Aquestes dues formen part del que s'anomenen Identitats notables, i admeten una demostració gràfica elemental en termes d'àrees de quadrats i rectangles, i volums de cubs i paral·lelepípedes.

Visualització de l'expansió fins a la quarta potència del binomi

La fórmula general utilitza nombres combinatoris, i diu:

${(a+b)}^{n}=\sum _{k=0}^{n}{n \choose k}a^{n-k}\,b^{k},\quad \quad \quad \quad \quad (1)$

on el coeficient binomial ${n \choose k}$ és el nombre combinatori definit com a ${n \choose k}={\frac {n!}{k!\,(n-k)!}}$, que es llegeix "$n$ sobre $k$". El conjunt dels coeficients binomials ordenats en fileres amb $n$ creixent de dalt a baix constitueixen l'anomenat triangle de Tartaglia, triangle de Pascal o triangle aritmètic.

Exemples:

• per $n=2$ : $(a+b)^{2}={2 \choose 0}a^{2}+{2 \choose 1}ab+{2 \choose 2}b^{2}=a^{2}+2ab+b^{2}$

• per $n=3$ : $(a+b)^{3}={3 \choose 0}a^{3}+{3 \choose 1}a^{2}b+{3 \choose 2}ab^{2}+{3 \choose 3}b^{3}=a^{3}+3a^{2}b+3ab^{2}+b^{3}$
• $12^{3}=(10+2)^{3}=10^{3}+3\ 10^{2}\ 2+3\ 10\ 2^{2}+2^{3}=1000+600+120+8=1728$

Quan tenim $(a-b)^{n}$, n'hi ha prou amb escriure-ho com a $(a+(-b))^{n}$, amb el que s'obté $(a-b)^{2}=a^{2}-2ab+b^{2}$, $(a-b)^{3}=a^{3}-3a^{2}b+3ab^{2}-b^{3}$ i, en general,

${(a-b)}^{n}=\sum _{k=0}^{n}(-1)^{k}{n \choose k}a^{n-k}\,b^{k}$.

La fórmula és molt anterior a Newton. La seva història pot trobar-se a l'article Potència d'un Binomi de R. Nolla esmentat més avall com a enllaç extern.

Demostració

Raonament combinatori

Tenint en compte l'expressió $x=(a+b)^{n}$, veiem que $x$ es pot escriure com el producte de $n$ binomis, $x=s_{1}s_{2}\cdots s_{n}$, on cada $s_{i}=a+b$, i el desenvolupament de $x$ és la suma de tots els productes formats agafant un terme – ja sigui $a$ o $b$ – de cada $s_{i}$. Per exemple, el terme $a^{n}$ en el desenvolupament de $x$ s'obté seleccionant $a$ en cada $s_{i}$.

El coeficient que multiplica cada terme del desenvolupament de $x$ queda determinat per la quantitat de formes diferents que hi ha per triar termes $s_{i}$ tals que el seu producte és de la mateixa forma que el terme (excloent el coeficient). En el cas de $t=a^{n-1}b$, $t$ es pot formar a base d'agafar $b$ d'un dels $s_{i}$ i $a$ de tota la resta. Hi ha $n$ formes de seleccionar un $s_{i}$ per obtenir la $b$; per tant $t$ s'obté de $n$ formes diferents en el desenvolupament de $x$, i per tant el seu coeficient és $n$. En general, per $t=a^{n-k}b^{k}$, hi ha

${n \choose k}$

Formes diferents de seleccionar els $s_{i}$ per obtenir els $b$s (ja que $k$ $b$s se seleccionen a partir de $n$ $s_{i}$), i per tant aquest ha de ser el coeficient per a $t$.

Demostració algebraica

Una altra forma de demostrar el teorema binomial és per inducció. Quan $n=0$, es té

$(a+b)^{0}=1=\sum _{k=0}^{0}{0 \choose k}a^{0-k}b^{k}.$

Per hipòtesi d'inducció se suposa que el teorema és veritat quan l'exponent val $m$. Llavors per $n=m+1$

$(a+b)^{m+1}=a(a+b)^{m}+b(a+b)^{m}\,$$=a\sum _{k=0}^{m}{m \choose k}a^{m-k}b^{k}+b\sum _{j=0}^{m}{m \choose j}a^{m-j}b^{j}$

Aplicant la propietat distributiva

$=\sum _{k=0}^{m}{m \choose k}a^{m-k+1}b^{k}+\sum _{j=0}^{m}{m \choose j}a^{m-j}b^{j+1}$

Traient fora del sumatori el terme $k=0$

$=a^{m+1}+\sum _{k=1}^{m}{m \choose k}a^{m-k+1}b^{k}+\sum _{j=0}^{m}{m \choose j}a^{m-j}b^{j+1}$

fent $j=k-1$

$=a^{m+1}+\sum _{k=1}^{m}{m \choose k}a^{m-k+1}b^{k}+\sum _{k=1}^{m+1}{m \choose k-1}a^{m-k+1}b^{k}$

Traient fora del sumatori de la dreta el terme $k=m+1$

$=a^{m+1}+\sum _{k=1}^{m}{m \choose k}a^{m-k+1}b^{k}+\sum _{k=1}^{m}{m \choose k-1}a^{m+1-k}b^{k}+b^{m+1}$

Combinant els sumatoris

$=a^{m+1}+b^{m+1}+\sum _{k=1}^{m}\left[{m \choose k}+{m \choose k-1}\right]a^{m+1-k}b^{k}$

Aplicant la regla de Pascal

$=a^{m+1}+b^{m+1}+\sum _{k=1}^{m}{m+1 \choose k}a^{m+1-k}b^{k}$

Afegint dins dels sumatori els termes $m+1$

$=\sum _{k=0}^{m+1}{m+1 \choose k}a^{m+1-k}b^{k}$

La sèrie binomial

Si escrivim $(a+b)^{n}=a^{n}(1+{\frac {b}{a}})^{n}$ podem anomenar $x={\frac {b}{a}}$ i escriure $\alpha$ en lloc de $n$. La funció $f(x)=(1+x)^{\alpha }$rep el nom de funció binomial i té sentit també si $\alpha$ és un nombre complex qualsevol. La seva sèrie de Mclaurin té radi de convergència més gran o igual que 1, segons el valor de $\alpha$, i es coneix com a sèrie binomial o expansió binomial. Aquesta generalitza el Binomi de Newton $(1)$, que és el cas en què $\alpha$ és un nombre natural.

${\begin{aligned}(1+x)^{\alpha }&=\sum _{k=0}^{\infty }\;{\alpha \choose k}\;x^{k}=1+\alpha x+{\frac {\alpha (\alpha -1)}{2!}}x^{2}+\cdots ,\end{aligned}}$

on ${\alpha \choose k}:={\frac {\alpha (\alpha -1)(\alpha -2)\cdots (\alpha -k+1)}{k!}}$, (regla mnemotècnica: hi ha $k$ factors en el numerador i $k$ factors en el denominador).

Per exemple, quan $\alpha =1/2$ i $|x|<1$ dona la sèrie següent:

${\sqrt {1+x}}=\textstyle 1+{\frac {1}{2}}x-{\frac {1}{8}}x^{2}+{\frac {1}{16}}x^{3}-{\frac {5}{128}}x^{4}+{\frac {7}{256}}x^{5}-\cdots$.

I quan $\alpha =-1/2$ i $|x|<1$;

${\frac {1}{\sqrt {1+x}}}=\textstyle 1-{\frac {1}{2}}x+{\frac {3}{8}}x^{2}-{\frac {5}{16}}x^{3}+{\frac {35}{128}}x^{4}-{\frac {63}{256}}x^{5}+\cdots$.

Observacions

A les demostracions anteriors es veu que és essencial la propietat commutativa $ab=ba$. Si, per exemple, $A$ i $B$ fossin dues matrius que no commutessin, aleshores tindríem simplement $(A+B)^{2}=A^{2}+AB+BA+B^{2}$ o $(A+B)^{3}=A^{3}+A^{2}B+ABA+BA^{2}+AB^{2}+BAB+B^{2}A+B^{3}$.

El Binomi de Newton és molt útil per al càlcul mental. Per exemple, calcular $21^{4}$ és molt fàcil si s'escriu com a $(20+1)^{4}$.

Observi's que la suma dels coeficients binomials del binomi de grau $n$ és igual a $2^{n}$i la suma dels coeficients que jauen en els llocs senars coincideix amb la suma dels que jauen en els llocs parells.

El terme ${n \choose k}a^{n-k}\,b^{k}$ quan $a=1-p$ i $b=p$ és la probabilitat que el nombre d'èxits sigui exactament $k$ en una seqüència de $n$ assaigs independents amb una probabilitat fixa $p$ d'ocurrència de l'èxit entre els assaigs. A aquesta distribució de probabilitat se li dona el nom de distribució binomial.

La primera aparició escrita de la sèrie binomial va ser en una carta de Newton a Henry Oldenburg, Secretari de la Royal Society, el 1676. Newton va usar el binomi i la distribució binomial el 1693 per a resoldre un problema sorgit en un joc de daus, per encàrrec de la casa reial de Guillem III.

Comentaris

És famós el vers del poeta portuguès Fernando Pessoa: O binómio de Newton é tão belo como a Vénus de Milo./ O que há é pouca gente para dar por isso. (El binomi de Newton és tan bell com la Venus de Milo./ El que passa és que poques persones ho noten.)

Un problema conegut, i no molt fàcil, de càlcul mental és l'anomenat Problema de Rachinsky, que consisteix a calcular mentalment ${\dfrac {10^{2}+11^{2}+12^{2}+13^{2}+14^{2}}{365}}$. Hi ha diverses maneres de fer-ho, però potser la mes ràpida és expressar els quadrats com a quadrats d'un binomi de manera que apareguin cancel·lacions. Aquest problema és el que apareix escrit a la pissarra al quadre Aritmètica mental. A l'escola pública de S. Rachinsky (1895), del pintor realista rus Nikolay Bogdanov-Belsky.

Vegeu també

• Triangle de Tartaglia
• Identitats notables
• Coeficient Binomial

Enllaços externs

• Potència d'un binomi, per R. Nolla