Diagrama de Coxeter-Dynkin


En geometria, un diagrama de Coxeter-Dynkin (diagrama de Coxeter, o graf de Coxeter), nomenat així pels matemàtics Donald Coxeter i Eugene Dynkin, és un graf amb arestes etiquetades numèricament (anomenades «branques») que representen les relacions espacials entre una col·lecció de miralls (o hiperplans reflectits). Això descriu una construcció calidoscòpica: cada «node» del graf representa un mirall (anomenat faceta) i l'etiqueta enganxada a la branca codifica l'ordre de l'angle díedre entre dos miralls (en una cresta de domini). Una branca no marcada representa implícitament ordre-3.
Cada diagrama representa un grup de Coxeter, i els grups de Coxeter estan classificats pels seus diagrames associats.
Els diagrames de Dynkin estan estretament relacionats, però difereixen dels diagrames de Coxeter en dos aspectes:
- en primer lloc, les branques etiquetades com a «4» o més grans són dirigides, mentre que els diagrames de Coxeter no són dirigides;
- en segon lloc, els diagrames Dynkin han de satisfer una restricció (cristal·logràfica) addicional, és a dir, que les úniques branques permeses són les etiquetades com 2, 3, 4 i 6.
Els diagrames Dynkin es corresponen i s'utilitzen per classificar els sistemes d'arrels i, per tant, les àlgebres de Lie semisimple.[1]
Descripció modifica
Les branques d'un diagrama de Coxeter-Dynkin estan etiquetades amb un nombre racional p, el que representa un angle diedre de 180°/p. Quan p = 2, l'angle és de 90° i els miralls no tenen cap interacció, de manera que la branca pot ser omesa del diagrama. Si una branca no està marcada, se suposa que té p = 3, el que representa un angle de 60°. Dos miralls paral·lels tenen una branca marcada amb «∞». En principi, n miralls poden ser representats per un graf complet en el qual es dibuixen totes les n(n - 1)/2 branques. A la pràctica, gairebé totes les configuracions interessants dels miralls inclouen una sèrie d'angles rectes, de manera que s'ometen les branques corresponents.
Els diagrames poden ser etiquetats per la seva estructura gràfica. Les primeres formes estudiades per Ludwig Schläfli són els ortoesquemes que tenen gràfics lineals que generen polítops regulars i tessel·lacions regulars. Els plagioesquemes són símplex representats pels grafs ramificats, i els cicloesquemes són símplex representats per grafs cicles.
La matriu de Schläfli modifica
Cada diagrama de Coxeter té una matriu de Schläfli corresponent amb elements de matriu ai,j = aj,i = -2cos (π / p), on p és l'ordre de la branca entre els parells de miralls. Com és una matriu de cosinus també s'anomena matriu de Gram. Totes les matrius de Schläfli del grup de Coxeter són simètriques perquè els seus vectors d'arrel estan normalitzats. Es relaciona estretament a la matriu de Cartan, que s'utilitza de forma similar, però els grafs dirigits dels diagrames de Dynkin estan limitats en els casos de p= 2, 3, 4 i 6, que en general NO són simètrics.
El determinant de la matriu de Schläfli, anomenat el Schläflià, i el seu signe determina si el grup és finit (positiu), afí (zero), indefinit (negatiu). Aquesta regla es denomina Criteri de Schläfli.[2]
Els valors propis de la matriu de Schläfli determina si un grup de Coxeter és de tipus finit (tots positius), afí (tot no negatiu, almenys un és zero), o de tipus indefinit (en cas contrari). El tipus indefinit de vegades se subdivideix, per exemple, en grups de Coxeter hiperbòlics i altres. No obstant això, hi ha múltiples definicions no equivalents per als grups de Coxeter hiperbòlics. Utilitzem la següent definició: Un grup de Coxeter amb el diagrama connectat és hiperbòlic si no és ni de tipus finit ni afí, però cada subdiagrama apropiat connectat és de tipus finit o afí.
Un grup de Coxeter hiperbòlic és compacte si tots els subgrups són finits (és a dir, tenen determinants positius), i paracompacte si tots els seus subgrups són finits o afíns (és a dir, tenen determinants no negatius). Els grups finits i afins també s'anomenen el·líptics i parabòlics, respectivament. Els grups hiperbòlics també s'anomenen Lannér i F. Lannér, qui va enumerar els grups hiperbòlics compactes el 1950,[3] i Koszul (o quasi-Lannér) per als grups paracompactes.
Grups de Coxeter de rang 2 modifica
Pel rang 2, la varietat d'un grup de Coxeter està totalment determinada pel determinant de la matriu Schläfli, ja que és simplement el producte dels valors propis:
- tipus finit (determinant positiu),
- tipus afí (determinant igual a zero),
- tipus hiperbòlic (determinant negatiu).
Coxeter utilitza una notació gràfica equivalent, que enumera les seqüències de l'ordre de ramificació com un substitut dels diagrames de grafs amb nodes i branques. També hi ha solucions racionals ([p/q] o ![]()
![]()
![]()
![]()
![]() ), amb mcd (p, q) = 1, que defineixen la superposició de dominis fonamentals. Per exemple, 3/2, 4/3, 5/2, 5/3, 5/4 i 6/5.
), amb mcd (p, q) = 1, que defineixen la superposició de dominis fonamentals. Per exemple, 3/2, 4/3, 5/2, 5/3, 5/4 i 6/5.
| Tipus | Finit | Afí | Hiperbòlic | |||||
|---|---|---|---|---|---|---|---|---|
| Geometria | 
|

|

|

|
... | 
|

|

|
| Coxeter | [ ] |
[2] |
[3] |
[4] |
[p] |
[∞] |
[∞] |
[iπ/λ] |
| Ordre | 2 | 4 | 6 | 8 | 2p | ∞ | ||
| Les línies de mirall són de color per correspondre als nodes del diagrama de Coxeter. Els dominis fonamentals estan acolorits alternativament. | ||||||||
| Ordre p |
Grup | Diagrama de Coxeter | Matriu de Schläfli | |||
|---|---|---|---|---|---|---|
| Determinant (4-a21*a₁₂) | ||||||
| Finit (Determinant > 0) | ||||||
| 2 | I₂(2) = A1xA1 | [2] | 4 | |||
| 3 | I₂(3) = A₂ | [3] | 3 | |||
| 3/2 | [3/2] | |||||
| 4 | I₂(4) = B₂ | [4] | 2 | |||
| 4/3 | [4/3] | |||||
| 5 | I₂(5) = H₂ | [5] | ~1.38196601125 | |||
| 5/4 | [5/4] | |||||
| 5/2 | [5/2] | ~3.61803398875 | ||||
| 5/3 | [5/3] | |||||
| 6 | I₂(6) = G₂ | [6] | 1 | |||
| 6/5 | [6/5] | |||||
| 8 | I₂(8) | [8] | ~0.58578643763 | |||
| 10 | I₂(10) | [10] | = ~0.38196601125 | |||
| 12 | I₂(12) | [12] | ~0.26794919243 | |||
| p | I₂(p) | [p] | ||||
| Afí (Determinant = 0) | ||||||
| ∞ | I₂(∞) = = | [∞] | 0 | |||
| Hiperbòlic (Determinant ≤ 0) | ||||||
| ∞ | [∞] | 0 | ||||
| ∞ | [iπ/λ] | |||||
Visualitzacions geomètriques modifica
El diagrama de Coxeter-Dynkin pot ser vist com un graf descriptiu del domini fonamental dels miralls. Un mirall representa un hiperplà en un espai esfèric, euclidià, o en un espai hiperbòlic; (en els espais 2D un mirall és una línia, i en 3D un mirall és un pla).
Aquestes visualitzacions mostren els dominis fonamentals dels grups euclidians 2D i 3D, i dels grups esfèrics 2D. Per a cada diagrama de Coxeter es pot deduir mitjançant la identificació els miralls hiperplans i l'etiquetatge de les seves connectivitats, fent cas omís dels angles diedres de 90° (ordre 2).
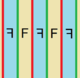
 Grups de Coxeter en el pla euclidià amb els diagrames equivalents. Les reflexions estan etiquetades en els nodes del graf, R1, R2, etc., i estan acolorides pel seu ordre reflexió. Les reflexions de 90° estan inactives, i per tant suprimides del diagrama. Els miralls paral·lels estan connectats per la branca etiquetada amb ∞. El grup prismàtic x es mostra com una duplicació de , però també es pot crear com a domini rectangular de la duplicació dels triangles . és una duplicació del triangle . | |
 Molts grups de Coxeter en el pla hiperbòlic es poden estendre a partir dels casos euclidians com una sèrie de solucions hiperbòliques. | |
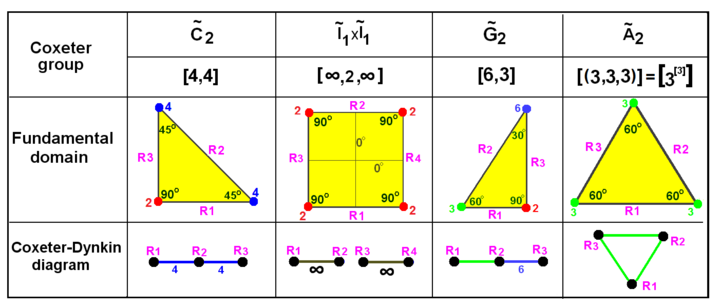
 Grups de Coxeter en espai 3D amb diagrames. Els miralls (cares triangulars) són etiquetats per 0..3 al vèrtex oposat. Les branques s'acoloreixen pel seu ordre reflexió.
|
 Grups de Coxeter en l'esfera amb diagrames equivalents. Un domini fonamental es resumeix en groc. Els vèrtexs del domini (i les branques del graf) s'acoloreixen pel seu ordre reflexió. |
Grups de Coxeter finits modifica
- Vegeu també famílies de polítops per a una taula de polítops uniformes de node final associats amb aquests grups.
- Es donen tres símbols diferents per als mateixos grups; una lletra / nombre, un conjunt de nombres entre claudàtors, i el diagrama de Coxeter.
- Els grups Dn bifurcats són la meitat o la versió alternada dels grups regulars Cn.
- Els grups Dn i En bifurcats també són etiquetats amb una forma superíndexada [3a,b,c], on a, b, c són els números de segments en cadascuna de les tres branques.
| Rang | Grups de Lie simple | Grups de Lie excepcionals | ||||||
|---|---|---|---|---|---|---|---|---|
| 1 | A1=[ ] |
|||||||
| 2 | A₂=[3] |
B₂=[4] |
D₂=A1A1 |
G₂=[6] |
H₂=[5] |
I₂[p] | ||
| 3 | A₃=[3²] |
B₃=[3,4] |
D₃=A₃ |
E₃=A₂A1 |
F₃=B₃ |
H₃ |
||
| 4 | A₄=[33] |
B₄=[3²,4] |
D₄=[31,1,1] |
E₄=A₄ |
F₄ |
H₄ | ||
| 5 | A₅=[34] |
B₅=[33,4] |
D₅=[32,1,1] |
E₅=D₅ |
||||
| 6 | A₆=[3⁵] |
B₆=[34,4] |
D₆=[33,1,1] |
E₆=[32,2,1] | ||||
| 7 | A₇=[3⁶] |
B₇=[3⁵,4] |
D₇=[34,1,1] |
E₇=[33,2,1] | ||||
| 8 | A₈=[37] |
B₈=[3⁶,4] |
D₈=[35,1,1] |
E₈=[34,2,1] | ||||
| 9 | A9=[38] |
B9=[37,4] |
D9=[36,1,1] |
|||||
| 10+ | .. | .. | .. | .. | ||||
Aplicació amb polítops uniformes modifica
Els diagrames de Coxeter-Dynkin poden enumerar explícitament gairebé totes les classes de polítops uniformes i mosaics uniformes. Cada polítop uniforme amb simetria de reflexió pura (tots, excepte uns pocs casos especials, tenen simetria de reflexió pura) pot ser representat per un diagrama de Coxeter-Dynkin amb permutacions de marques. Cada polítop uniforme pot ser generat utilitzant aquest tipus de miralls i un únic punt generador; les imatges del mirall creen nous punts com reflexos, i llavors els polítops arestes poden ser definits entre els punts i un punt de la imatge del mirall. Les cares poden ser construïdes per cicles d'arestes creades, etc. Per especificar la generació del vèrtex, un o més nodes estan marcats amb els anells, el que significa que el vèrtex no està dins del mirall(s), representat per node(s) amb anell(s); si dos o més miralls estan marcats, el vèrtex és equidistant a ells. Un mirall és actiu (crea reflexions) només pel que fa als punts, no en ell. Un diagrama necessita almenys un node actiu per representar un polítop.
Tots els polítops regulars, representats pel símbol de Schläfli {p, q, r, ...}, poden tenir els seus dominis fonamentals representats per un conjunt de n miralls relacionats amb un diagrama de Coxeter-Dynkin d'una línia de nodes i branques etiquetades per p, q, r, ..., amb el primer node anellat.
Els polítops uniformes amb un anell corresponen al generador de punts en els cantons del domini fonamental símplex. Dos anells corresponen a les arestes del símplex i tenen un grau de llibertat, amb només el punt mitjà com la solució uniforme per a la mateixa longitud de l'aresta. En general, el generador de punts de k-anells estan en (k-1)-cares del símplex, i si tots el nodes estan anellats, el punt generador està a l'interior del símplex.
Un marcat secundari transmet un cas especial de polítops uniformes amb simetria no-reflectiva. Aquests casos existeixen com a alternatives de polítops de simetria de reflexió. Aquest marcat elimina el punt central d'un node anellat, anomenat «forat» (cercles amb nodes esborrats), que dona a entendre que els nodes alternatius han sigut eliminats. El polítop resultant tindrà una subsimetria del grup de Coxeter original. Una truncació alternada s'anomena «xato».
- Un únic node representa un sol mirall; això s'anomena grup A1. Si el node amb anell crea un segment lineal perpendicular al mirall, es representa com {}.
- Dos nodes no units representen dos miralls perpendiculars. Si tots dos nodes tenen un anell es pot crear un rectangle, o un quadrat si el punt està a la mateixa distància de tots dos miralls.
- Dos nodes connectats per una branca d'ordre n pot crear un n-gon si el punt està en un mirall, i un 2n-gon si el punt està fora de tots dos miralls. Això forma el grup I1 (n).
- Dos miralls paral·lels poden representar un polígon infinit, formant el grup I1 (∞), també anomenat Ĩ1.
- Tres miralls en triangle formen imatges vistes en un calidoscopi tradicional i es poden representar per tres nodes connectats a un triangle. Repetint aquest model s'obtenen branques etiquetades com (3 3 3), (4 4 2), (3 2 6), encara que els dos últims es poden dibuixar com una línia (amb les dues branques ignorades). Aquestes generaran tessel·lats regulars.
- Tres miralls poden generar políedres uniformes; inclosos els nombres racionals dona el conjunt de triangles de Schwarz.
- Tres miralls, amb un perpendicular als altres dos, poden formar els prismes regulars.
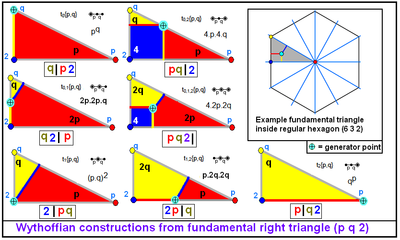 En general, hi ha 7 construccions uniformes reflectores dins d'un triangle, a partir de 7 posicions topològiques del generador dins el domini fonamental. Cada mirall actiu té un generador en un vèrtex, amb dos miralls actius es tenen generadors en els costats, i tres miralls actius es té el generador a l'interior. Es poden resoldre un o dos graus de llibertat per una posició única per a longituds de les arestes del poliedre resultant o de la tessel·lació. |
 Exemple 7 generadors en simetria octaèdrica, domini fonamental del triangle (4 3 2), amb generació d'1/8 xato com una alternança. |
De vegades, els polítops uniformes dobles es marquen amb una barra perpendicular en substitució del nodes anellats, i una barra per als forats del nodes xatos. Per exemple, ![]()
![]()
![]() representa un rectangle (com dos miralls ortogonals actius), i
representa un rectangle (com dos miralls ortogonals actius), i ![]()
![]()
![]() representa el seu polígon dual, el rombe.
representa el seu polígon dual, el rombe.
Exemple de políedres i tessel·lats modifica
Per exemple, el grup Coxeter B₃ té un diagrama ![]()
![]()
![]()
![]()
![]() ; això també es diu simetria octaèdrica.
; això també es diu simetria octaèdrica.
Hi ha 7 políedres uniformes convexes que es poden construir a partir d'aquest grup de simetria i 3 a partir de les seves subsimetries de les seves alternances, cada un amb un diagrama de Coxeter-Dynkin marcat de manera única cap amunt. El símbol de Wythoff representa un cas especial del diagrama de Coxeter de grafs de rang 3, amb totes les branques d'ordre 3 etiquetades, en lloc de suprimir les banques d'ordre 2. El símbol de Wythoff és capaç de manejar la forma xata, però no les alternances generals i sense tots els nodes anellats.
| Políedres octaèdrics uniformes | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Simetria: [4,3], (*432) | [4,3]+ (432) |
[1+,4,3] = [3,3] (*332) |
[3+,4] (3*2) | |||||||
| {4,3} | t{4,3} | r{4,3} r{31,1} |
t{3,4} t{31,1} |
{3,4} {31,1} |
rr{4,3} s₂{3,4} |
tr{4,3} | sr{4,3} | h{4,3} {3,3} |
h₂{4,3} t{3,3} |
s{3,4} s{31,1} |
= |
= |
= |
||||||||
| Duals de políedres uniformes | ||||||||||
| V43 | V3.8² | V(3.4)² | V4.6² | V34 | V3.43 | V4.6.8 | V34.4 | V33 | V3.6² | V3⁵ |
Les mateixes construccions es poden fer en grups de Coxeter inconnexos (ortogonals) com els prismes uniformes, i es pot veure més clarament com mosaics de diedres i hosohedres sobre l'esfera, com la família [6] × [ ] o [6,2] :
| Políedres esfèrics diedres hexagonals uniformes | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Simetria: [6,2], (*622) | [6,2]+, (622) | [6,2+], (2*3) | ||||||||||||

|

|

|

|
|

|

| ||||||||
| {6,2} | t{6,2} | r{6,2} | t{2,6} | {2,6} | rr{6,2} | tr{6,2} | sr{6,2} | s{2,6} | ||||||
| Duals dels políedres uniformes | ||||||||||||||

|

|

|

|

|

|

|

|

| ||||||
| V6² | V12² | V6² | V4.4.6 | V2⁶ | V4.4.6 | V4.4.12 | V3.3.3.6 | V3.3.3.3 | ||||||
En comparació, la família [6,3], ![]()
![]()
![]()
![]()
![]() produeix un conjunt paral·lel de 7 tessel·lats uniformes del pla euclidià i el seu tessel·lat dual. També en aquest cas hi ha 3 alternances i alguna versió de mitja simetria.
produeix un conjunt paral·lel de 7 tessel·lats uniformes del pla euclidià i el seu tessel·lat dual. També en aquest cas hi ha 3 alternances i alguna versió de mitja simetria.
| Políedres hexagonals uniformes / Tessel·lats triangulars | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Simetria: [6,3], (*632) | [6,3]+ (632) |
[6,3+] (3*3) | |||||||||
| {6,3} | t{6,3} | r{6,3} | t{3,6} | {3,6} | rr{6,3} | tr{6,3} | sr{6,3} | s{3,6} | |||

|

|

|

|

|

|

|

|

| |||
| 63 | 3.12² | (3.6)² | 6.6.6 | 3⁶ | 3.4.12.4 | 4.6.12 | 3.3.3.3.6 | 3.3.3.3.3.3 | |||
| Duals dels políedres uniformes | |||||||||||

|

|

|

|

|

|

|

|

| |||
| V63 | V3.12² | V(3.6)² | V63 | V3⁶ | V3.4.12.4 | V.4.6.12 | V34.6 | V3⁶ | |||
En el pla hiperbòlic [7,3], ![]()
![]()
![]()
![]()
![]() la família produeix un conjunt paral·lel de tessel·lats uniformes del pla euclidià i el seu tessel·lat dual. Només ha 1 alternança (xata), ja que tots els ordres de ramificació són imparells. Moltes altres famílies hiperbòliques dels tessel·lats uniformes es poden veure en els tessel·lats uniformes en pla hiperbòlic.
la família produeix un conjunt paral·lel de tessel·lats uniformes del pla euclidià i el seu tessel·lat dual. Només ha 1 alternança (xata), ja que tots els ordres de ramificació són imparells. Moltes altres famílies hiperbòliques dels tessel·lats uniformes es poden veure en els tessel·lats uniformes en pla hiperbòlic.
| Políedres heptagonals uniformes / Tessel·lats triangulars | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Simetria: [7,3], (*732) | [7,3]+, (732) | ||||||||||

|

|

|

|

|

|

|

| ||||
| {7,3} | t{7,3} | r{7,3} | t{3,7} | {3,7} | rr{7,3} | tr{7,3} | sr{7,3} | ||||
| Duals dels políedres uniformes | |||||||||||

|

|

|

|

|

|

|

| ||||
| V73 | V3.14.14 | V3.7.3.7 | V6.6.7 | V37 | V3.4.7.4 | V4.6.14 | V3.3.3.3.7 | ||||
Grups de Coxeter afins modifica
Les famílies del tessel·lats euclidians convexos regulars es defineixen pels grups de Coxeter afins. Aquests grups són idèntics als grups finits amb la inclusió d'un node afegit. Els nom de les lletres se'ls dona la mateixa lletra amb un ~ per sobre de la lletra. L'índex es refereix al grup finit, de manera que el rang és l'índex més 1 (els símbols d'Ernst Witt per als grups afins es donen com «també» entre parèntesis).
- : els diagrames d'aquest tipus són cicles. (també Pn)
- : està associat amb la família de tessel·lació hipercúbica regular {4, 3, ...., 4}. (també Rn)
- : relacionats amb C per un mirall eliminat. (també Sn)
- : relacionats amb C per dos miralls eliminats. (també Qn)
- , , . (també T₇, T₈, T9)
- : formes de la tessel·lació regular {3,4,3,3}. (també U₅)
- : formes del domini fonamental del triangle 30-60-90. (també V₃)
- : són dos miralls paral·lels. (= = ) (també W₂)
Els grups compostos també es poden definir com a projeccions ortogonals. L'ús més comú , com ![]()
![]()
![]()
![]()
![]()
![]()
![]() representa els dominis d'un tauler d'escacs quadrat o rectangular al pla euclidià.
representa els dominis d'un tauler d'escacs quadrat o rectangular al pla euclidià. ![]()
![]()
![]()
![]()
![]()
![]()
![]() representa els dominis fonamentals del prisma triangular en el 3-espai euclidià.
representa els dominis fonamentals del prisma triangular en el 3-espai euclidià.
| Rang | (P2+) | (S4+) | (R2+) | (Q5+) | (Tn+1) / (U₅) / (V₃) |
|---|---|---|---|---|---|
| 2 | =[∞] |
=[∞] |
|||
| 3 | =[3[3]] * |
=[4,4] * |
=[6,3] * | ||
| 4 | =[3[4]] * |
=[4,31,1] * |
=[4,3,4] * |
=[31,1,3−1,31,1] |
|
| 5 | =[3[5]] * |
=[4,3,31,1] * |
=[4,3²,4] * |
=[31,1,1,1] * |
=[3,4,3,3] * |
| 6 | =[3[6]] * |
=[4,3²,31,1] * |
=[4,33,4] * |
=[31,1,3,31,1] * |
|
| 7 | =[3[7]] * |
=[4,33,31,1] |
=[4,34,4] |
=[31,1,3²,31,1] |
=[32,2,2] |
| 8 | =[3[8]] * |
=[4,34,31,1] * |
=[4,3⁵,4] |
=[31,1,33,31,1] * |
=[33,3,1] * |
| 9 | =[3[9]] * |
=[4,3⁵,31,1] |
=[4,3⁶,4] |
=[31,1,34,31,1] |
=[35,2,1] * |
| 10 | =[3[10]] * |
=[4,3⁶,31,1] |
=[4,37,4] |
=[31,1,3⁵,31,1] | |
| 11 | ... | ... | ... | ... |
Grups de Coxeter hiperbòlics modifica
Hi ha molts grups de Coxeter hiperbòlics infinits. Els grups hiperbòlics es classifiquen en compactes o no, amb els grups compactes que tenen dominis fonamentals delimitats. Existeixen grups hiperbòlics compactes símplex (Lannér símplex) amb rang de 3 a 5. Els grups paracompactes símplex (Koszul símplex) existeixen fins al rang 10. Els grups supercompactes (polítops Vinberg) han estat explorats però encara no s'han determinat totalment. En 2006, Allcock va demostrar que hi ha un nombre infinit de polítops Vinberg compactes per dimensions superiors a 6, i un nombre infinit de volums finits per politops Vinberg per a dimensions superiors a 19,[4] pel que una enumeració completa no és possible. Tots aquests dominis reflectants fonamentals, tant símplex com no-símplex, es solen anomenar «politops Coxeter» o, de vegades amb menys precisió, «políedres Coxeter».
Grups hiperbòlics en H² modifica
| Exemple de triangles rectangles [p,q] | ||||
|---|---|---|---|---|
 [3,7] |
 [3,8] |
 [3,9] |
 [3,∞] | |
 [4,5] |
 [4,6] |
 [4,7] |
 [4,8] |
 [∞,4] |
 [5,5] |
 [5,6] |
 [5,7] |
 [6,6] |
 [∞,∞] |
| Exemple de triangles generals [(p,q,r)] | ||||
 [(3,3,4)] |
 [(3,3,5)] |
 [(3,3,6)] |
 [(3,3,7)] |
 [(3,3,∞)] |
 [(3,4,4)] |
 [(3,6,6)] |
 [(3,∞,∞)] |
 [(6,6,6)] |
 [(∞,∞,∞)] |
Existeixen grups triangulars bidimensionals hiperbòlics com diagrames de Coxeter de rang 3, definits pel triangle (p q r) per a:
Hi ha un nombre infinit de grups de Coxeter triangulars hiperbòlics compactes, inclòs els grafs lineals i triangulars. Existeixen els grafs lineals per triangles rectangles (amb r = 2).[5]
| Lineal | Cíclic | ||||
|---|---|---|---|---|---|
| ∞ [p,q], 2(p+q)<pq
|
∞ [(p,q,r)],
|
Existeixen grups de Coxeter paracompactes de rang 3 com a límits als compactes.
| Grafs lineals | Grafs cíclics |
|---|---|
|
|
Grups triangulars aritmètics modifica
Els grups triangulars hiperbòlics que també són grups aritmètics formen un subconjunt finit. Kisao Takeuchi va determinar la llista completa amb ordinador i la va publicar en el seu Arithmetic triangle groups, 1977 (Grups triangulars aritmètics).[6] Hi ha un total de 85 (76 compactes i 9 paracompactes).
| Triangles rectangles (p q 2) | Triangles generals (p q r) |
|---|---|
Grups compactes: (76)
Triangles rectangles paracompactes: (4)
|
Triangles generals: (39)
Triangles generals paracompactes: (5)
|
|
|
Polígons hiperbòlics Coxeter per sobre dels triangles modifica
Es poden construir altres calidoscopis hiperbòlics H² a partir de polígons d'ordre superior.
Aquests calidoscopis poden ser identificats com a grups triangulars per una seqüència cíclica d'interseccions de miralls d'ordres al voltant del domini fonamental, com (a b c d ...) o de forma equivalent en notació orbifold com * abcd....
Els diagrames de Coxeter-Dynkin per aquests calidoscopis poligonals poden ser vists com un domini fonamental degenerat (n-1)-símplex amb una cicle de branques ordenades a, b, c ... i les restants n*(n-3)/2 branques estan etiquetades com a infinit (∞) que representen els miralls que no es tallen. L'únic exemple no-hiperbòlic és la simetria euclidiana de quatre miralls en un quadrat o un rectangle com ![]()
![]()
![]()
![]()
![]()
![]()
![]() , [∞, ∞, 2] (orbifold *2222).
, [∞, ∞, 2] (orbifold *2222).
Una altra representació de la branca de miralls que no es tallen, donada per Vinberg, són branques infinites o línies de punts discontínues, de manera que aquest diagrama es pot mostrar com ![]()
![]()
![]() , amb les quatre branques d'ordre-2 suprimides en tot el perímetre. Per exemple, un domini de quadrilàter (a b c d) tindrà dues branques d'ordre infinit que connecten miralls ultraparal·lels. L'exemple hiperbòlic més petit és
, amb les quatre branques d'ordre-2 suprimides en tot el perímetre. Per exemple, un domini de quadrilàter (a b c d) tindrà dues branques d'ordre infinit que connecten miralls ultraparal·lels. L'exemple hiperbòlic més petit és ![]()
![]()
![]()
![]()
![]()
![]()
![]() , [∞, 3, ∞] o [iπ/λ1,3,iπ/λ₂] (orbifold *3222), on (λ1, λ₂) són la distància entre els miralls ultraparal·lels. L'expressió alternativa és
, [∞, 3, ∞] o [iπ/λ1,3,iπ/λ₂] (orbifold *3222), on (λ1, λ₂) són la distància entre els miralls ultraparal·lels. L'expressió alternativa és ![]()
![]()
![]() , amb tres branques d'ordre-2 suprimides al voltant del perímetre. De la mateixa manera (2 3 2 3) (orbifold *3232) es pot representar com
, amb tres branques d'ordre-2 suprimides al voltant del perímetre. De la mateixa manera (2 3 2 3) (orbifold *3232) es pot representar com ![]()
![]()
![]() , i (3 3 3 3) (orbifold *3333) es pot representar com un gràfic complet
, i (3 3 3 3) (orbifold *3333) es pot representar com un gràfic complet ![]()
![]()
![]() . El domini del quadrilàter més gran (∞ ∞ ∞ ∞) és un quadrat infinit, representat per un graf tetraèdric complet amb un perímetre de 4 branques com vèrtexs ideals i dues branques diagonals com infinit (que es mostren com a línies de punts) per als miralls ultraparal·lels:
. El domini del quadrilàter més gran (∞ ∞ ∞ ∞) és un quadrat infinit, representat per un graf tetraèdric complet amb un perímetre de 4 branques com vèrtexs ideals i dues branques diagonals com infinit (que es mostren com a línies de punts) per als miralls ultraparal·lels: ![]()
![]()
![]()
![]()
![]() .
.
Grups hiperbòlics compactes (Grups Lannér símplex) modifica
Els grups hiperbòlics compactes també s'anomenen Grups Lannér, perquè Folke Lannér va ser el primer que els va estudiar el 1950.[7] Només existeixen grafs de rang 4 i 5. Coxeter va estudiar els grups de Coxeter hiperbòlics lineals en Regular Honeycombs in hyperbolic space, 1954 (Tessel·lacions regulars en l'espai hiperbòlic),[8] que incloïa dues solucions racionals en 4-espai hiperbòlic: [5/2,5,3,3] = ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() i [5,5/2,5,3] =
i [5,5/2,5,3] = ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
Rangs 4–5 modifica
El domini fonamental de qualsevol dels dos grups bifurcants, [5,31,1] i [5,3,31,1], és el doble que el corresponent als grups lineals [5,3,4] i [5,3,3,4], respectivament. Els noms de les lletres es donen per Johnson, ampliats amb símbols de Witt.[9]
| Dimensió Hd |
Rang | Recompte total | Lineal | Bifurcat | Cíclic |
|---|---|---|---|---|---|
| H3 | 4 | 9 | = [4,3,5]: |
= [5,31,1]: |
= [(33,4)]: |
| H4 | 5 | 5 | = [33,5]: |
= [5,3,31,1]: |
= [(34,4)]: |
Grups hiperbòlics paracompactes (Grups Koszul símplex) modifica

Els grups de Coxeter hiperbòlics paracompactes (també anomenats no-compactes) contenen subgrups afins i tenen dominis fonamentals asimptòtics símplex. El rang més alt d'un grup hiperbòlic paracompacte és 10. Aquests grups s'anomenen així pel matemàtic francès Jean-Louis Koszul.[10] També se'ls anomena grups quasi-Lannér per ser una extensió dels grups Lannér compactes. M. Chein va determinar la llista completa amb ordinador i la va publicar el 1969.[11]
Per Vinberg, tots menys vuit d'aquests 72 grups compactes i paracompactes símplex són aritmètics. Dos dels grups no-aritmètics són compactes: ![]()
![]()
![]()
![]()
![]() i
i ![]()
![]()
![]()
![]()
![]()
![]() . Els altres sis grups no-aritmètics són tots paracompactes, amb cinc grups de 3 dimensions,
. Els altres sis grups no-aritmètics són tots paracompactes, amb cinc grups de 3 dimensions, ![]()
![]()
![]()
![]()
![]()
![]()
![]() ,
, ![]()
![]()
![]()
![]()
![]() ,
, ![]()
![]()
![]()
![]()
![]()
![]()
![]() ,
, ![]()
![]()
![]()
![]()
![]() , i
, i ![]()
![]()
![]()
![]()
![]() , i un grup de 5 dimensions,
, i un grup de 5 dimensions, ![]()
![]()
![]()
![]()
![]()
![]() .
.
Símplex ideal modifica




 , [(∞, ∞, ∞)] vist en el model del Disc de Poincaré
, [(∞, ∞, ∞)] vist en el model del Disc de PoincaréHi ha 5 grups de Coxeter hiperbòlics que expressen símplex ideals, grafs on s'elimina qualsevol node resultat en un grup de Coxeter afí. Així, tots els vèrtexs d'aquest símplex ideals són a l'infinit.[12]
| Rang | Grup ideal | Subgrups afins | ||
|---|---|---|---|---|
| 3 | [(∞,∞,∞)] | [∞] | ||
| 4 | [4[4]] | [4,4] | ||
| 4 | [3[3,3]] | [3[3]] | ||
| 4 | [(3,6)[2]] | [3,6] | ||
| 6 | [(3,3,4)[2]] | [4,3,3,4], [3,4,3,3] | ||
Rangs 4–10 modifica

Hi ha un total de 58 grups de Coxeter hiperbòlics paracompactes de rang de 4 a 10. Els 58 s'agrupen en cinc categories. Els símbols de les lletres són donats pel matemàtic Johnson com a símbols de Witt ampliats, utilitzant PQRSTWUV com afins als símbols de Witt i afegint LMNOXYZ. Aquests grups hiperbòlics se'ls dona una línia alta, o barret, per cicloesquemes. La sintaxi de claudàtor per Coxeter és una representació linealitzada del grup de Coxeter.
| Rang | Recompte total | Grups | |||
|---|---|---|---|---|---|
| 4 | 23 |
= [(3,3,4,4)]: |
= [3,3[3]]: |
= [3,4,4]: |
= [3[]x[]]: |
| 5 | 9 |
= [3,3[4]]: |
= [4,3,((4,2,3))]: |
= [(3,4)²]: |
= [4,31,1,1]: |
| 6 | 12 |
= [3,3[5]]: |
= [4,3,32,1]: |
= [33,4,3]: |
= [32,1,1,1]: = [4,3,31,1,1]: |
| 7 | 3 |
= [3,3[6]]: |
= [31,1,3,32,1]: |
= [4,3²,32,1]: |
|
| 8 | 4 | = [3,3[7]]: |
= [31,1,3²,32,1]: |
= [4,33,32,1]: |
= [33,2,2]: |
| 9 | 4 | = [3,3[8]]: |
= [31,1,33,32,1]: |
= [4,34,32,1]: |
= [34,3,1]: |
| 10 | 3 | = [ | = [31,1,34,32,1]: |
= [4,3⁵,32,1]: |
= [36,2,1]: |
Les relacions dels subgrups dels grups hiperbòlics paracompactes modifica
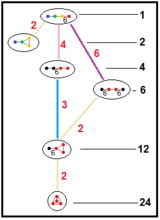
Aquests arbres representen les relacions dels subgrups dels grups hiperbòlics paracompactes. Els índexs dels subgrups en cada connexió s'indiquen en vermell.[13] Els subgrups d'índex 2 representen un mirall eliminat i una duplicació del domini fonamental. Altres poden ser inferides per commensurabilitat (quocient sencer de volums) per als dominis de tetraedres.
| H3 | 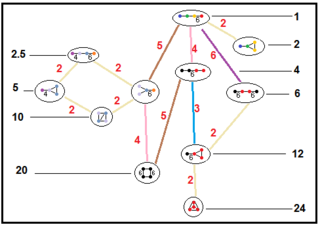
|
|

|

|
|---|---|---|---|---|
| H4 | 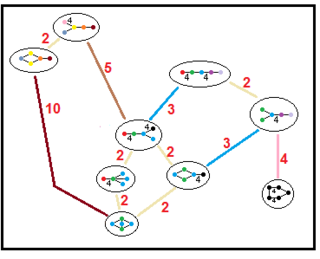
| |||
| H⁵ | 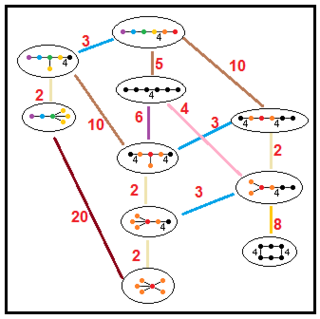
|
Grups Coxeter hipercompactes (Polítops de Vinberg) modifica
Igual que el pla hiperbòlic H² té dominis poligonals no-triangulars, també existeixen dimensions superiors en els dominis hiperbòlics reflexius. Aquests dominis no-símplex es poden considerar símplex degenerats amb miralls que no es creuen donat ordre infinit, o en un diagrama de Coxeter, com branques dibuixades com línies de punts o discontínues. Aquests dominis es diuen polítops de Vinberg no-símplex, per Ernest Vinberg pel seu algorisme de Vinberg per trobar dominis fonamentals no-símplex d'un grup de reflexió hiperbòlic. Geomètricament aquests dominis fonamentals poden ser classificats com a piràmides, o prismes o altres polítops amb les arestes com la intersecció de dos miralls que tenen angles diedres com π/n per n = 2,3,4 ...
En un domini basat-símplex, hi ha n + 1, miralls per espai n-dimensional. En els dominis no-símplex, hi ha més de n + 1 miralls. La llista és finita, però no del tot coneguda. En comptes de fer llistes parcials, s'han enumerat com «n + k miralls» per k miralls, com 2, 3 i 4.
Els grups de Coxeter hipercompactes en un espai tridimensional o superior difereixen de dos grups dimensionals en un aspecte essencial. Dos n-gons hiperbòlics tenen els mateixos angles en el mateix ordre cíclic, però poden tenir diferents longituds d'aresta i en general no són congruents. En contrast, els polítops de Vinberg en 3 dimensions o superiors estan completament determinats pels angles diedres. Aquest fet es basa en el teorema de rigidesa de Mostow, en què els dos grups isomorfs generats per les reflexions en Hn per n ≥ 3 defineixen dominis fonamentals congruents (polítops de Vinberg).
Polítops de Vinberg amb rang n + 2 per a espais n-dimensionals modifica
En 1996, Esselmann va enumerar la llista completa de polítops de Vinberg hiperbòlics compactes amb rang n + 2 miralls per n-dimensions.[14] Sr. I. Kaplinskaya va publicar una llista parcial el 1974.[15] En 2003, P. Tumarkin va publicar la llista completa de les solucions paracompactes per a dimensions de 3 a 17.[16]
La forma paracompacte més petita en H3 pot ser representada per ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() o [∞, 3,3, ∞], que pot ser construïda per un mirall eliminat del grup hiperbòlic paracompacte [3,4,4] com [3,4,1 +, 4 ].
o [∞, 3,3, ∞], que pot ser construïda per un mirall eliminat del grup hiperbòlic paracompacte [3,4,4] com [3,4,1 +, 4 ].
El domini fonamental duplicat canvia d'un tetràedre a una piràmide quadrangular. Altres piràmides inclouen [4,4,1 +, 4] = [∞, 4,4, ∞], ![]()
![]()
![]()
![]()
![]()
![]()
![]() =
= ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() . Eliminant un mirall d'alguns dels gràfs hiperbòlics cíclics de Coxeter es converteixen en grafs papallona: [(3,3,4,1 +, 4)] = [((3, ∞, 3)), ((3, ∞, 3))] o
. Eliminant un mirall d'alguns dels gràfs hiperbòlics cíclics de Coxeter es converteixen en grafs papallona: [(3,3,4,1 +, 4)] = [((3, ∞, 3)), ((3, ∞, 3))] o ![]()
![]()
![]()
![]()
![]() ; [(3,4,4,1 +, 4)] = [((4, ∞, 3)), ((3, ∞, 4))] o
; [(3,4,4,1 +, 4)] = [((4, ∞, 3)), ((3, ∞, 4))] o ![]()
![]()
![]()
![]()
![]() ; [(4,4,4, 1 +, 4)] = [((4, ∞, 4)), ((4, ∞, 4))] o
; [(4,4,4, 1 +, 4)] = [((4, ∞, 4)), ((4, ∞, 4))] o ![]()
![]()
![]()
![]()
![]() .
.
Altres gràfs paracompactes vàlids amb la piràmide quadrangular dels dominis fonamentals inclouen:
| Dimensió | Rang | Grafs |
|---|---|---|
| H3 | 5 |
|
Un altre subgrup és [1+,41,1,1] = [∞,4,1+,4,∞] = [∞[6]]; ![]()
![]()
![]()
![]()
![]() =
= ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() =
= ![]()
![]()
![]()
![]()
![]()
![]()
![]() .[17]
.[17]
Polítops de Vinberg amb rang n + 3 per a espais n-dimensionals modifica
Hi ha un nombre finit de símplex fonamentals degenerats per sobre de 8-dimensions. El 2004, P. Tumarkin va enumerar la llista completa dels polítops compactes de Vinberg amb rang n + 3 miralls de n-dimensions. Aquests grups estan marcats per línies de punts o trencada per branques ultraparal·leles. La llista completa de polítops no-compactes de Vinberg amb rang n + 3 miralls i amb un vèrtex no símplex per n-dimensions va ser enumerada per Mike Roberts.[18]
De grups de Coxeter de 4 a 8 dimensions, rangs de 7 a 11, hi ha 44, 16, 3, 1, i 1 respectivament.[19] El més alt va ser descobert per Bugaenko el 1984, la dimensió 8, rang 11:[20]
| Dimensions | Rang | Casos | Grafs | ||
|---|---|---|---|---|---|
| H4 | 7 | 44 | ... | ||
| H⁵ | 8 | 16 | .. | ||
| H⁶ | 9 | 3 | |||
| H7 | 10 | 1 | |||
| H8 | 11 | 1 | |||
Polítops de Vinberg amb rang n + 4 per a espais n-dimensionals modifica
Hi ha un nombre finit de símplex fonamentals degenerats per sobre de 8-dimensions. Els polítops compactes de Vinberg amb rang n + 4 miralls de n-dimensions han estat explorats per A. i P. Felikson Tumarkin en 2005.[21]
Grups Lorentzians modifica
 {3,3,7} en 3-espai hiperbòlic, fent la intersecció de l'enrajolat amb el pla infinit, en el model de semiespai de Poincaré. |
 {7,3,3} vist des de l'exterior del model de bola de Poincaré. |

 , [3[3,3,3]] és un subrup d'índex 120 de [6,3,3,3].
, [3[3,3,3]] és un subrup d'índex 120 de [6,3,3,3].Els grups lorentzians per a dominis símplex es poden definir en forma de grafs més enllà de les formes hiperbòliques paracompactes. De vegades es denominen símplex súper ideals i també estan relacionades amb una geometria Lorentziana, anomenada així per Hendrik Lorentz en el camp de la relativitat especial i general de l'espaitemps, que conté un (o més) components tridimensionals en el temps amb els seus productes escalars negatius.[9] Danny Calegari els anomena «grups de Coxeter cocompactes convexos en espai hiperbòlic n-dimensional».[22][23]
En 1982, George Maxwell va enumerar una llista finita de Lorentz dels rangs 5 a 11 en el document Sphere Packings and Hyperbolic Reflection Groups (Esfera embalatge i grups de reflexió hiperbòlics). Ell diu que en el nivell 2, l'expulsió de tota permutació de 2 nodes deixa un gràfic finit o euclidià. La seva enumeració és completa, però no va incloure els grafs que són un subgrup d'un altre.
Totes les branques d'ordre superior dels grups de Coxeter de rang 4 són de Lorentz, que acaben en el límit com un diagrama de Coxeter-Dynkin d'un graf complet 3-símplex amb 6 branques d'ordre infinit, que pot expressar-se com [∞[3,3]].
Els rangs 5-11 tenen un nombre finit de grups lorentzians: 186, 66, 36, 13, 10, 8 i 4 grups respectivament.[24]
En 2013, H. Chen i J.P. Labbé, van tornar a calcular i publicar la llista completa en el document Lorentzian Coxeter groups and Boyd. Maxwell ball packings (Grups de Coxeter Lorentzians i de Boyd. Envasos de boles Maxwell).[25]
Per als rangs més alts de 8-11, les llistes completes són:
| Rang | Recompte total | Grups | ||||
|---|---|---|---|---|---|---|
| 4 | ∞ | [3,3,7] ... [∞,∞,∞]: [4,3[3]] ... [∞,∞[3]]: | ||||
| 5 | 186 | ...[3[3,3,3]]: |
||||
| 6 | 66 | |||||
| 7 | 36 | [31,1,1,1,1,1]: | ||||
| 8 | 13 |
[3,3,3[6]]: |
[4,3,3,33,1]: |
[4,3,3,32,2]: | ||
| 9 | 10 |
[3,3[3+4],3]: |
[32,1,3²,32,1]: |
[33,1,33,4]: [33,1,3,3,31,1]: |
[33,3,2]: [32,2,4]: | |
| 10 | 8 | [3,3[8],3]: [3,3[3+5],3]: |
[32,1,33,32,1]: |
[35,3,1]: [33,1,34,4]: |
[34,4,1]: | |
| 11 | 4 | [32,1,34,32,1]: |
[32,1,3⁶,4]: [32,1,3⁵,31,1]: |
[37,2,1]: | ||
Diagrames Coxeter molt estesos modifica
Un ús inclou una definició molt estesa de l'ús directe del diagrama de Dynkin que considera com a grups afins com estesos, grups hiperbòlics sobre-estesos, i un tercer node com a grups simples molt estesos. Aquestes extensions solen marcar un exponent de 1, 2 o 3 + símbols per al nombre de nodes estesos. Aquestes sèries esteses es poden estendre cap enrere, per eliminació seqüencial dels nodes de la mateixa posició en el gràfic, tot i que el procés s'atura després de l'eliminació de node de ramificació. La família estesa E₈ és l'exemple més comú que mostra que s'estén cap enrere des d'E₃ i cap endavant a E11.
El procés que s'estén es pot definir com una sèrie limitada de grafs de Coxeter que progressen de finit cap afí cap hiperbòlic cap a grup de Lorentz. El determinant de les matrius de Cartan determina on els canvis de la sèrie finita (positiu) per afí (zero) per hiperbòlica (negativa), i acaba com un grup de Lorentz, que conté almenys un subgrup hiperbòlic.[26] Els grups no-cristalogràfics Hn formen una sèrie estesa on H₄ s'estén com una hiperbòlica compacta i es troba sobre-estesa en un grup de Lorentz.
Els determinants de la matriu de Schläfli per rang es:[27]
- det(A1n=[2n-1]) = 2n (finit per tot n).
- det(An=[3n-1]) = n+1 (finit per tot n).
- det(Bn=[4,3n-2]) = 2 (finit per tot n).
- det(Dn=[3n-3,1,1]) = 4 (finit per tot n).
Els determinants de la matriu Schläfli en sèrie excepcionals són:
- det(En=[3n-3,2,1]) = 9-n (finit per E₃(=A₂A1), E₄(=A₄), E₅(=D₅), E₆, E₇ i E₈, afí a E9 (), i hiperbòlic a E10).
- det([3n-4,3,1]) = 2(8-n) (finit per n=4 fins a 7, afí a (), i hiperbòlic a n=8).
- det([3n-4,2,2]) = 3(7-n) (finit per n=4 fins a 6, afí a (), i hiperbòlic a n=7).
- det(Fn=[3,4,3n-3]) = 5-n (finit per F₃(=B₃) fins a F₄, afí a F₅ (), i hiperbòlic a F₆).
- det(Gn=[6,3n-2]) = 3-n (finit per G₂, afí a G₃ (), i hiperbòlic a G₄).
| Finit | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Rang n | [3[7],3n-7] | [4,33,3n-6,1] | [31,1,3,3,3n-6,1] | [3n-5,2,2] | [3[8],3n-8] | [4,34,3n-7,1] | [31,1,3,3,3,3n-7,1] | [3n-5,3,1] | En=[3n-4,2,1] |
| 3 | [3−1,2,1] E₃=A₂A1 | ||||||||
| 4 | [3−1,2,2] A₂² |
[3−1,3,1] A₃A1 |
[30,2,1] E₄=A₄ | ||||||
| 5 | [4,3,3,3,3−1,1] B₄A1 |
[31,1,3,3,3−1,1] D₄A1 |
[30,2,2] A₅ |
[30,3,1] A₅ |
[31,2,1] E₅=D₅ | ||||
| 6 | [3⁵] A₆ |
[4,34] B₆ |
[31,1,3,3,3] D₆ |
[31,2,2] E₆ |
[4,3,3,3,3,3−1,1] B₅A1 |
[31,1,3,3,3,3−1,1] D₅A1 |
[31,3,1] D₆ |
[32,2,1] E₆ * | |
| 7 | [3[7]] A₆+= |
[4,33,31,1] B₆+= |
[31,1,3,3,31,1] D₆+= |
[32,2,2] E₆+= |
[3⁶] A₇ |
[4,3⁵] B₇ |
[31,1,3,3,3,30,1] D₇ |
[32,3,1] E₇ * |
[33,2,1] E₇ * |
| 8 | [3[7],3] A₆++= |
[4,33,32,1] B₆++= |
[31,1,3,3,32,1] D₆++= |
[33,2,2] E₆++= |
[3[8]] A₇+= * |
[4,34,31,1] B₇+= * |
[31,1,3,3,3,31,1] D₇+= * |
[33,3,1] E₇+= * |
[34,2,1] E₈ * |
| 9 | [3[7],3,3] A₆+++ |
[4,33,33,1] B₆+++ |
[31,1,3,3,33,1] D₆+++ |
[34,2,2] E₆+++ |
[3[8],3] A₇++= * |
[4,34,32,1] B₇++= * |
[31,1,3,3,3,32,1] D₇++= * |
[34,3,1] E₇++= * |
[35,2,1] E9=E₈+= * |
| 10 | [3[8],3,3] A₇+++ * |
[4,34,33,1] B₇+++ * |
[31,1,3,3,3,33,1] D₇+++ * |
[35,3,1] E₇+++ * |
[36,2,1] E10=E₈++= * | ||||
| 11 | [37,2,1] E11=E₈+++ * | ||||||||
| Det(Mn) | 7(7-n) | 2(7-n) | 4(7-n) | 3(7-n) | 8(8-n) | 2(8-n) | 4(8-n) | 2(8-n) | 9-n |
Plegat geomètric modifica
| φA : AΓ --> AΓ' per a tipus finits | |||
|---|---|---|---|
| Γ | Γ' | Descripció del plegat | Diagrames Coxeter–Dynkin |
| I₂(h) | Γ(h) | Plegat dièdric | 
|
| Bn | A2n | (I,sn) | |
| Dn+1, A2n-1 | (A₃,+/-ε) | ||
| F₄ | E₆ | (A₃,±ε) | |
| H₄ | E₈ | (A₄,±ε) | |
| H₃ | D₆ | ||
| H₂ | A₄ | ||
| G₂ | A₅ | (A₅,±ε) | |
| D₄ | (D₄,±ε) | ||
| φ: AΓ+ --> AΓ'+ per a tipus afins | |||
| Localment trivial | 
| ||
| (I,sn) | |||
| , | (A₃,±ε) | ||
| , | (A₃,±ε) | ||
| (I,sn) | |||
| (I,sn) & (I,s0) | |||
| (A₃,ε) & (I,s0) | |||
| (A₃,ε) & (A₃,ε') | |||
| (A₃,-ε) & (A₃,-ε') | |||
| (I,s1) | |||
| , | (A₃,±ε) | ||
| , | (A₅,±ε) | ||
| , | (B₃,±ε) | ||
| , | (D₄,±ε) | ||
Un digrama de Coxeter-Dynkin, lligat simplement, (finit, afí, o hiperbòlic) que té una simetria (que satisfà una condició, a continuació) es pot quocientar per una simetria, produint un nou diagrama, en general, multiplicant els llaços, amb el procés anomenat «plegat».[29][30]
Per exemple, en D₄ plegat a G₂, la vora en els punts G₂ de la classe dels 3 nodes exteriors (valència 1), a la classe del node central (valència 3).
Geomètricament això correspon a les projeccions ortogonals de polítops uniformes i tessel·lats. En particular, qualsevol diagrama de Coxeter-Dynkin finit lligat simplement, es pot plegar per I₂(h), on h és el nombre de Coxeter, que correspon geomètricament a una projecció al pla de Coxeter.
 Uns quants plecs hiperbòlics |
Reflexions complexes modifica
El diagrama de Coxeter-Dynkin s'ha estès a l'espai complex Cn, on els nodes són reflexos unitaris de període superior a 2. Els nodes estan etiquetats per un índex, que es presumeix 2 per a la reflexió real ordinària si es suprimeix. Coxeter escriu el grup complex p[q]r, amb el diagrama ![]()
![]()
![]()
![]()
![]() .[31]
.[31]
Un polítop regular complex 1-dimensional en es representa com ![]() , tenint p vèrtexs. La seva representació real és un polígon regular, {p}. La seva simetria és p [] o
, tenint p vèrtexs. La seva representació real és un polígon regular, {p}. La seva simetria és p [] o ![]() , d'ordre p. Un operador unitari generador per
, d'ordre p. Un operador unitari generador per ![]() es veu com una rotació en per 2π / p radians en sentit horari, i es crea una vora
es veu com una rotació en per 2π / p radians en sentit horari, i es crea una vora ![]() per les aplicacions seqüencials d'una sola reflexió unitària. Un generador de reflexió unitària per a un 1-polítop amb p vèrtexs és e2πi / p = cos (2π / p) + i sin (2π / p). Quan p = 2, el generador és eπi = -1, el mateix que un punt reflectit en el pla real.
per les aplicacions seqüencials d'una sola reflexió unitària. Un generador de reflexió unitària per a un 1-polítop amb p vèrtexs és e2πi / p = cos (2π / p) + i sin (2π / p). Quan p = 2, el generador és eπi = -1, el mateix que un punt reflectit en el pla real.
En un polítop més alt, p{} o ![]() , representa un element p-vora, amb una 2-vora, {} o
, representa un element p-vora, amb una 2-vora, {} o ![]() , el que representa un avantatge real habitual entre el dos vèrtexs.
, el que representa un avantatge real habitual entre el dos vèrtexs.
 Els 1-polítops complexos representats en el pla d'Argand com polígons regulars per p = 2, 3, 4, 5, i 6, amb vèrtexs negres. El centroide dels p vèrtexs s'ha representat amb un punt vermell. Els costats dels polígons representen una aplicació del generador de simetria, el mapeig de cada vèrtex a la següent còpia en sentit antihorari. Aquests costats poligonals no tenen elements de vora del politop; un 1-polítop complex no pot tenir vores (que sovint és una vora complexa) i només conté elements de vèrtex. |
 Els 12 grups de Shephard irreductibles amb les relacions amb els índexs dels seus subgrups.[32] Els subgrups d'índex 2 es relacionen mitjançant l'eliminació d'un reflex real: p[2q]₂ --> p[q]p, índex 2. p[4]q --> p[q]p, índex q. |
 Subgrups p[4]₂ : p=2,3,4... p[4]₂ --> [p], índex p p[4]₂ --> p[]×p[], índex 2 |
Els polígons regulars complexos en tenen la forma p{q}r o el diagrama de Coxeter ![]()
![]()
![]()
![]()
![]() . El grup de simetria d'un polígon regular complex
. El grup de simetria d'un polígon regular complex ![]()
![]()
![]()
![]()
![]() no s'anomena en el grup de Coxeter, però sí en el grup Shephard, un tipus de grup de reflexió complexa. L'ordre de p[q]r és .[33]
no s'anomena en el grup de Coxeter, però sí en el grup Shephard, un tipus de grup de reflexió complexa. L'ordre de p[q]r és .[33]
El rang 2 dels grups de Shephard són: ₂[q]₂, p[4]₂, ₃[3]₃, ₃[6]₂, ₃[4]₃, ₄[3]₄, ₃[8]₂, ₄[6]₂, ₄[4]₃, ₃[5]₃, ₅[3]₅, ₃[10]₂, ₅[6]₂, i ₅[4]₃; o ![]()
![]()
![]() ,
, ![]()
![]()
![]() ,
, ![]()
![]()
![]() ,
, ![]()
![]()
![]() ,
, ![]()
![]()
![]() ,
, ![]()
![]()
![]() ,
, ![]()
![]()
![]() ,
, ![]()
![]()
![]() ,
, ![]()
![]()
![]() ,
, ![]()
![]()
![]() ,
, ![]()
![]()
![]() ,
, ![]()
![]()
![]() ,
, ![]()
![]()
![]() ,
, ![]()
![]()
![]() d'ordre 2q, 2p², 24, 48, 72, 96, 144, 192, 288, 360, 600, 1200, i 1800 respectivament.
d'ordre 2q, 2p², 24, 48, 72, 96, 144, 192, 288, 360, 600, 1200, i 1800 respectivament.
El grup de simetria p1[q]p₂ és representat per dos generadors R1, R₂, on: R1p1 = R₂p₂ = I. Si q és parell, (R₂R1)q/2 = (R1R₂)q/2. Si q és senar, (R₂R1)(q-1)/2R₂ = (R1R₂)(q-1)/2R1. Quan q és senar, p1=p₂.
El grup ![]()
![]()
![]() o [1 1 1]p és definit per tres períodes de dues reflexions unitàries {R1, R₂, R₃}: R1² = R1² = R₃² = (R1R₂)3 = (R₂R₃)3 = (R₃R1)3 = (R1R₂R₃R1)p = 1. El període p també és conegut com a doble rotació en real.
o [1 1 1]p és definit per tres períodes de dues reflexions unitàries {R1, R₂, R₃}: R1² = R1² = R₃² = (R1R₂)3 = (R₂R₃)3 = (R₃R1)3 = (R1R₂R₃R1)p = 1. El període p també és conegut com a doble rotació en real.
El grup semblant ![]()
![]()
![]() o [1 1 1](p) és definit per tres períodes de dues reflexions unitàries {R1, R₂, R₃}: R1² = R1² = R₃² = (R1R₂)3 = (R₂R₃)3 = (R₃R1)3 = (R1R₂R₃R₂)p = 1.
o [1 1 1](p) és definit per tres períodes de dues reflexions unitàries {R1, R₂, R₃}: R1² = R1² = R₃² = (R1R₂)3 = (R₂R₃)3 = (R₃R1)3 = (R1R₂R₃R₂)p = 1.
Referències modifica
- ↑ Hall, Brian C. Lie Groups, Lie Algebras, and Representations: An Elementary Introduction. Springer, 2003. ISBN 0-387-40122-9.
- ↑ Coxeter, Regular Polytopes, (3rd edition, 1973), Dover edition, ISBN 0-486-61480-8, Sec 7.7. page 133, Schläfli's Criterion
- ↑ Lannér F., On complexes with transitive groups of automorphisms, Medd. Lunds Univ. Mat. Sem. [Comm. Sem. Math. Univ. Lund], 11 (1950), 1–71
- ↑ Allcock, Daniel «Infinitely many hyperbolic Coxeter groups through dimension 19». Geometry & Topology, 10, 11-07-2006, pàg. 737–758. DOI: 10.2140/gt.2006.10.737.
- ↑ The Geometry and Topology of Coxeter Groups, Michael W. Davis, 2008 p. 105 Table 6.2. Hyperbolic diagrams
- ↑ «TAKEUCHI : Arithmetic triangle groups». Projecteuclid.org. [Consulta: 5 juliol 2013].
- ↑ Folke Lannér, On complexes with transitive groups of automorphisms, Comm. Sém., Math. Univ. Lund [Medd. Lunds Univ. Mat. Sem.] 11 (1950) [1]
- ↑ Regular Honeycombs in hyperbolic space Arxivat 2016-06-10 a Wayback Machine., Coxeter, 1954
- ↑ 9,0 9,1 Norman Johnson, Geometries and Transformations, Chapter 13: Hyperbolic Coxeter groups, 13.6 Lorentzian lattices
- ↑ J. L. Koszul, Lectures on hyperbolic Coxeter groups, University of Notre Dame (1967)
- ↑ M. Chein, Recherche des graphes des matrices de Coxeter hyperboliques d'ordre ≤10, Rev. Française Informat. Recherche Opérationnelle 3 (1969), no. Ser. R-3, 3–16 (French). [2]
- ↑ Subalgebras of hyperbolic Kay-Moody algebras, Figure 5.1, p.13
- ↑ N.W. Johnson, R. Kellerhals, J.G. Ratcliffe,S.T. Tschantz, Commensurability classes of hyperbolic Coxeter groups H3: p130, H4: p137, H⁵: p 138. [3]
- ↑ F. Esselmann, The classification of compact hyperbolic Coxeter d-polytopes with d+2 facets. Comment. Math. Helvetici 71 (1996), 229–242. [4]
- ↑ I. M. Kaplinskaya, Discrete groups generated by reflections in the faces of simplicial prisms in Lobachevskian spaces. Math. Notes,15 (1974), 88–91. [5]
- ↑ P. Tumarkin, Hyperbolic Coxeter n-polytopes with n+2 facets (2003)
- ↑ Norman W. Johnson and Asia Ivic Weiss, Quadratic Integers and Coxeter Groups, Canad. J. Math. Vol. 51 (6), 1999 pp. 1307–1336 [6] Arxivat 2014-03-26 a Wayback Machine.
- ↑ [7] A Classification of Non-Compact Coxeter Polytopes with n+3 Facets and One Non-Simple Vertex
- ↑ P. Tumarkin, Compact hyperbolic Coxeter (2004)
- ↑ V. O. Bugaenko, Groups of automorphisms of unimodular hyperbolic quadratic forms over the ring Zh√5+12 i. Moscow Univ. Math. Bull. 39 (1984), 6-14.
- ↑ Anna Felikson, Pavel Tumarkin, On compact hyperbolic Coxeter d-polytopes with d+4 facets, 2005 [8]
- ↑ Random groups, diamonds and glass, Danny Calegari of the University of Chicago, juny 25, 2014 at the Bill Thurston Legacy Conference
- ↑ Coxeter groups and random groups, Danny Calegari, last revised 4 Apr 2015
- ↑ George Maxwell, Sphere Packings and Hyperbolic Reflection Groups, JOURNAL OF ALGEBRA 79,78-97 (1982) [9]
- ↑ Hao Chen, Jean-Philippe Labbé, Lorentzian Coxeter groups and Boyd-Maxwell ball packings, http://arxiv.org/abs/1310.8608
- ↑ Kac-Moody Algebras in M-theory
- ↑ Cartan–Gram determinants for the simple Lie groups, Wu, Alfred C. T, The American Institute of Physics, Nov 1982
- ↑ John Crisp, 'Injective maps between Artin groups', in Down under group theory, Proceedings of the Special Year on Geometric Group Theory, (Australian National University, Canberra, Australia, 1996), Postscript Arxivat 2005-10-16 a Wayback Machine., pp 13-14, and googlebook, Geometric group theory down under, p 131
- ↑ Zuber, Jean-Bernard. Generalized Dynkin diagrams and root systems and their folding, p. 28–30. «citeseerx (10.1.1.54.3122)»
- ↑ Dechant, Pierre-Philippe; Boehm, Celine; Twarock, Reidun. Affine extensions of non-crystallographic Coxeter groups induced by projection, 25 octubre 2011.
- ↑ Coxeter, Complex Regular Polytopes, second edition, (1991)
- ↑ Coxeter, Complex Regular Polytopes, p. 177, Table III
- ↑ Unitary Reflection Groups, p.87
Bibliografia modifica
- Coxeter, Harold Scott MacDonald. Regular Polytopes (en anglès). Dover edition, 1973. ISBN 0-486-61480-8. «Capítol 5: The Kaleidoscope, and secció 11.3 Representation by graphs»
- Coxeter, Harold Scott MacDonald; Moser, W.O.J. Generators and Relations for Discrete Groups (en anglès). Nova York: Springer-Verlag, 1980.
- Coxeter, Harold Scott MacDonald. The Beauty of Geometry: Twelve Essays (en anglès). Dover Publications, 1999. ISBN 978-0-486-40919-1. «Capítol 3: Wythoff's Construction for Uniform Polytopes»
- Humphreys, James E. Reflection Groups and Coxeter Groups (en anglès). Cambridge studies in advanced mathematics, 29, 1990.
- Johnson, Norman W.; Kellerhals, Ruth; Ratcliffe, J. G; Tschantz, S. T. Transformation Groups. Vol. 4, The size of a hyperbolic Coxeter simplex (en anglès), 1999 [Consulta: 23 gener 2017]. Arxivat 2014-02-23 a Wayback Machine.
- Johnson, Norman W; Weiss, Asia Ivic. Quadratic Integers and Coxeter Groups, vol 51 (6) (en anglès). Canadian Mathematical Society, 1999.
- Johnson, Norman W. Geometries and Transformations (en anglès), 2011. «ca. 11, 12 i 13»
- Sherk, F. Arthur; McMullen, Peter; Thompson, Anthony C; Weiss, Asia Ivic. Kaleidoscopes: Selected Writings of H.S.M. Coxeter (en anglès). Wiley-Interscience Publication, 1995. ISBN 978-0-471-01003-6.
Vegeu també modifica
Enllaços externs modifica
- Weisstein, Eric W., «Coxeter–Dynkin diagram» a MathWorld (en anglès).
- October 1978 discussion on the history of the Coxeter diagrams by Coxeter and Dynkin in Toronto, Canada; Eugene Dynkin Collection of Mathematics Interviews, Cornell University Library.
![{\displaystyle \left[{\begin{matrix}2&a_{12}\\a_{21}&2\end{matrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/609b9b4324da49c4903330c430b14203d6f971cb)
![{\displaystyle \left[{\begin{smallmatrix}2&0\\0&2\end{smallmatrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/58d402f7fd38428fe2ac791f5a5d12bf7832c69f)
![{\displaystyle \left[{\begin{smallmatrix}2&-1\\-1&2\end{smallmatrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/18cb26b504d63dba11f3a12c7ee8fa25fe3bdf0a)
![{\displaystyle \left[{\begin{smallmatrix}2&1\\1&2\end{smallmatrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/838a30dc9d065ec434dff490bd84061ed569db3b)
![{\displaystyle \left[{\begin{smallmatrix}2&-{\sqrt {2}}\\-{\sqrt {2}}&2\end{smallmatrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/934421fb85592c1788a92b7d350953dd2ca94b5e)
![{\displaystyle \left[{\begin{smallmatrix}2&{\sqrt {2}}\\{\sqrt {2}}&2\end{smallmatrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4f92222bfe2eeefe46dddcc56620241d8efd5ef1)
![{\displaystyle \left[{\begin{smallmatrix}2&-\phi \\-\phi &2\end{smallmatrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/db286eb5ca733d2b6ab1c5f194f03593440b5b3a)

![{\displaystyle \left[{\begin{smallmatrix}2&\phi \\\phi &2\end{smallmatrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3dcf61f3b1fac33acafec6ac2d577c66f9f69306)
![{\displaystyle \left[{\begin{smallmatrix}2&1-\phi \\1-\phi &2\end{smallmatrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4a16582176db9cb488aa850d0b0a970ff0a62cd6)

![{\displaystyle \left[{\begin{smallmatrix}2&\phi -1\\\phi -1&2\end{smallmatrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8548776ee20b1e4a17df57227d372025e5bcbd65)
![{\displaystyle \left[{\begin{smallmatrix}2&-{\sqrt {3}}\\-{\sqrt {3}}&2\end{smallmatrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3b77e92921199a57f051014d4938de1a0d22ef38)
![{\displaystyle \left[{\begin{smallmatrix}2&{\sqrt {3}}\\{\sqrt {3}}&2\end{smallmatrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/51483cac6134b485a8a8ea0d9e2fee62fda6d13a)
![{\displaystyle \left[{\begin{smallmatrix}2&-2\cos(\pi /8)\\-2\cos(\pi /8)&2\end{smallmatrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/aa253a5d705d6109194b3afc3fe1d07614f51096)

![{\displaystyle \left[{\begin{smallmatrix}2&-2\cos(\pi /10)\\-2\cos(\pi /10)&2\end{smallmatrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c3bd41acbb86ee3d9cdaf3b56cd15f8dd58b4766)


![{\displaystyle \left[{\begin{smallmatrix}2&-2\cos(\pi /12)\\-2\cos(\pi /12)&2\end{smallmatrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2169b8ecb32a8780141f79c1340adff5c4eea986)

![{\displaystyle \left[{\begin{smallmatrix}2&-2\cos(\pi /p)\\-2\cos(\pi /p)&2\end{smallmatrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/71dd5a3c2a3aa08ab89d00e05a0afe4db4876ff8)



![{\displaystyle \left[{\begin{smallmatrix}2&-2\\-2&2\end{smallmatrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cd86323eaf497d2bb96f757556dd458abd5863cf)
![{\displaystyle \left[{\begin{smallmatrix}2&-2cosh(2\lambda )\\-2cosh(2\lambda )&2\end{smallmatrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/274a1c42213fa3aad2dd64c4b63f424d5f3ed349)
























































































































































































