Mètode de Graham
El mètode de Graham (Graham scan) és un mètode de càlcul computacional de l'envolupant convexa d'un grup finit de punts en el pla, amb una complexitat computacional O(n log n). El nom fa honor a Ronald Graham, qui va publicar l'algorisme el 1972.[1] L'algorisme calcula tots els vèrtexs de l'envolupant convexa ordenats al llarg de la frontera. Pot ser modificat fàcilment per trobar els punts que, sense ser vèrtexs, pertanyen a aquesta envolupant.
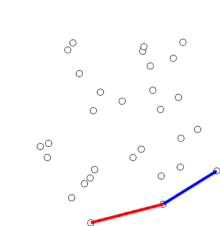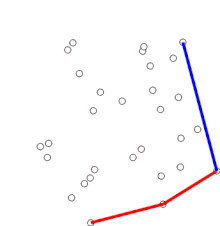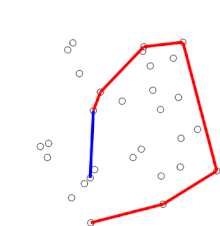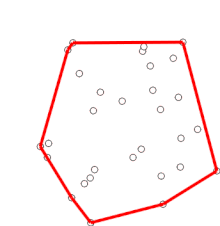
Procediment
modificaEs comença pel punt de més avall (el punt amb menor coordenada en l'eix Y), al que anomenarem origen. Llavors s'ordena la distribució de punts basant-se en l'angle entre el punt origen i tots els altres punts. Després de l'ordenament, es va punt per punt eliminant aquells que no es troben a l'envolupant convexa. Generalment, aquest procés es fa en el sentit antihorari.
Si un angle entre tres punts gira cap a dins, això implica que la forma no és convexa, de manera que podem treure aquest resultat. Podem trobar si una rotació és antihorària amb funcions trigonomètriques o mitjançant un producte creuat:
Si el resultat d'aquesta funció és 0, els punts són col·lineals, si és positiva vol dir que van en sentit antihorari, i si és negativa en sentit horari. No volem rotacions en sentit horari, ja que impliquen que estem en un angle interior.[1]
Variants
modificaLa mateixa idea també funciona si els punts s'ordenen segons la seva coordenada X en lloc de l'angle, i el casc es calcula en dos passos produint la part superior i la inferior del casc respectivament. Aquesta modificació va ser ideada per A. M. Andrew[2] i té les mateixes propietats bàsiques que l'algorisme de Graham.[3]
La tècnica d'escaneig utilitzada en el mètode de Graham és molt similar a la del problema de valors petits més propers, així que el mètode es pot utilitzar juntament amb algorismes paral·lels per calcular eficientment cascos convexos de seqüències ordenades de punts.[4]
Vegeu també
modificaReferències
modifica- ↑ 1,0 1,1 Graham, R.L. «An Efficient Algorithm for Determining the Convex Hull of a Finite Planar Set» (PDF). Information Processing Letters, 1, 4, 1972, pàg. 132–133. DOI: 10.1016/0020-0190(72)90045-2.
- ↑ Andrew, A. M. «Another efficient algorithm for convex hulls in two dimensions». Information Processing Letters, 9, 5, 1979, pàg. 216–219. DOI: 10.1016/0020-0190(79)90072-3.
- ↑ De Berg, Mark; Cheong, Otfried; Van Kreveld, Marc; Overmars. Computational Geometry Algorithms and Applications. Berlin: Springer, Overmars, p. 2–14. DOI 10.1007/978-3-540-77974-2. ISBN 978-3-540-77973-5.
- ↑ Berkman, Omer; Schieber, Baruch; Vishkin, Uzi «Optimal double logarithmic parallel algorithms based on finding all nearest smaller values». Journal of Algorithms, 14, 3, 1993, pàg. 344–370. DOI: 10.1006/jagm.1993.1018. CiteSeerX: 10.1.1.55.5669
Enllaços externs
modifica- Podeu veure una descripció acurada i exemples en diversos llenguatges de programació de l'Algorisme de cadena monòtona de A. M. Andrew a Wikibooks (anglès)