Moment magnètic
| Aquest article o secció no cita les fonts o necessita més referències per a la seva verificabilitat. |
En física, el moment magnètic o moment dipolar magnètic[1] és una mesura de la força d'una font magnètica. En el cas més simple d'una sola espira, el moment magnètic es defineix com:[2]
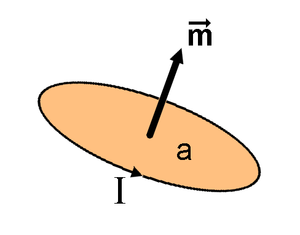 Moment magnètic m generat per un corrent d'intensitat I circulant en una espira d'àrea a | |
| Unitats | ampere metre quadrat |
|---|---|
| Fórmula | |
on
- a és el vector àrea d'una espira, mentre el corrent elèctric I és constant.
La direcció del vector àrea vindrà donada per la regla de la mà dreta, si tanquem els dits en la direcció del corrent, el dir gros apuntarà en la direcció de a. La posició de la mà seria com si féssim autoestop.
En el cas més complicat d'un sòlid carregat que gira, el moment magnètic pot ser determinat seguint la següent equació:
on
- J és la densitat de corrent
El moment magnètic a un camp magnètic és una mesura del flux magnètic establert per la rotació d'una càrrega elèctrica en un camp magnètic. El moment és negatiu, això indica que és diamagnètic, i igual a l'energia de rotació dividida pel camp magnètic.
En física atòmica i nuclear, el moment magnètic es representa amb el símbol m i es mesura en magnetons de Bohr, és associat amb el gir intrínsec (espín) i amb el moviment orbital de la partícula a un sistema.
Per a un sistema de càrregues, el moment magnètic es determina sumant les contribucions individuals de cada càrrega-massa-radi que el componen.
El moment dipolar magnètic d‟un objecte determina la magnitud del parell que aquest experimenta en un camp magnètic determinat. Els objectes amb moments magnètics més grans experimenten parells de torsió més grans quan s'aplica el mateix camp magnètic. La força (i la direcció) d'aquest parell no sols depèn de la magnitud del moment magnètic, sinó també de la seva orientació pel que fa a la direcció del camp magnètic. Per tant, el moment magnètic es pot considerar un vector. La direcció del moment magnètic apunta del pol sud al pol nord de l'imant (dins l'imant).
El camp magnètic d'un dipol magnètic és proporcional al seu moment dipolar magnètic. La component dipolar del camp magnètic d'un objecte és simètrica respecte a la direcció del seu moment dipolar magnètic i disminueix amb la galleda inversa de la distància a l'objecte.
Explicació
modificaEl moment magnètic pot ser explicat amb d'un imant en forma de barra que té pols magnètics d'igual magnitud però de polaritat oposada. Cada pol és la font d'una força magnètica que disminueix amb la distància. Com que els pols magnètics venen per parelles, les seves forces interfereixen entre elles perquè mentre un pol atreu l'altre repel·leix. Aquesta interferència és més gran com més a prop són els pols, per exemple quan l'imant és molt curt. La força magnètica produïda per una barra d'imant, a un punt de l'espai, depèn de dos factors, de la força p dels seus pols i de la distància d que els separa. La força és proporcional al producte
,
on descriu el "moment magnètic" o "moment dipolar" de l'imant al llarg de la distància R i la seva direcció com l'angle entre R i l'eix de l'imant.
Qualsevol objecte carregat en rotació, des dels quarks fins als cúmuls de galàxies, tenen moment magnètic.
Sobre la relació entre el moment magnètic i la magnetització vegeu magnetització.
El magnetisme pot ser creat pel corrent elèctric en circular per espires i bobines, així qualsevol corrent que circula per una espira plana produeix un moment magnètic i la seva magnitud és igual al producte del corrent i l'àrea de l'espira. Quan una partícula qualsevol és en rotació, es comporta com una espira i presenta un moment magnètic.
L'equació per al moment magnètic per a una espira per la que passa un corrent elèctric i un vector àrea la magnitud vindrà donada per:
on
- és el moment magnètic, un vector mesurat en ampere-metre quadrat,[3][4] o de manera equivalent en joules per tesla,[5]
- és el corrent, un escalar mesurat en amperes, i
- és el vector àrea de l'espira, tenim que x, y, i z són les coordenades i l'àrea en metres quadrats de la projecció de l'espira sobre els plans yz-, zx-, i xy-.
Mesurament
modificaEls moments magnètics dels objectes es mesuren típicament amb dispositius anomenats magnetòmetres, encara que no tots els magnetòmetres mesuren el moment magnètic: Alguns estan configurats per mesurar camp magnètic al seu lloc. Si el camp magnètic que envolta un objecte es coneix prou bé, aleshores el moment magnètic es pot calcular a partir d'aquest camp magnètic.
El moment magnètic a un camp magnètic
modificaEl moment magnètic d'un objecte és un vector que relaciona el moment o "parell de gir" alineat en un camp magnètic que experimenta l'objecte cap al mateix camp vectorial. la relació vindrà donada per
on
- és el parell de gir o moment, mesurat en newton-metre,
- és el moment magnètic, mesurat en ampere-metre quadrat, i
- és el camp magnètic, mesurat en newton per (ampere-metre).
L'alineament del moment magnètic amb el camp crea una diferència d'energia potencial U:
El moment magnètic és una quantitat que descriu la força magnètica de tot un objecte. De vegades, però, és útil o necessari saber quant del moment magnètic net de l'objecte és produït per una porció particular d'aquest imant. Per tant, és útil definir el camp de magnetització M com:
on mΔV i VΔV són el moment dipolar magnètic i el volum d'una porció prou petita de l'imant ΔV. Aquesta equació es representa sovint utilitzant notació derivada tal que
on dm és el moment magnètic elemental i dV és l'element de volum. El moment magnètic net de l'imant m és per tant
on la integral triple denota integració sobre el volum de l'imant. Per a la magnetització uniforme (on tant la magnitud i la direcció de M és el mateix per a tot l'imant (com un imant de barra recta) la darrera equació se simplifica a:
on V és el volum de la barra magnètica.
No obstant això, la magnetització sovint no apareix com un paràmetre del material per als materials ferromagnètics comercialment disponibles. En el seu lloc, el paràmetre que apareix és la densitat de flux residual (o romanència), denotada Br. La fórmula necessària en aquest cas per calcular m a (unitats de A⋅m2) és:
on:
Moment magnètic de spin
modificaEls electrons i molts nuclis atòmics també tenen moments magnètics intrínsecs, l'explicació dels quals requereixi tractament mecano-quàntic i que es relaciona amb el moment angular de les partícules. Són aquests moments magnètics intrínsecs els que donen lloc a efectes macroscòpics de magnetisme, i a altres fenòmens com la ressonància magnètica nuclear.
El moment magnètic d'espín és una propietat intrínseca o fonamental de les partícules, com la massa o la càrrega elèctrica. Aquest moment està relacionat amb el fet que les partícules elementals tenen moment angular intrínsec o espín, per a partícules carregades això porta inevitablement al fet que es comportin de manera similar a un petit circuit amb càrregues en moviment. No obstant això, també existeixen partícules neutres sense càrrega elèctrica com el neutró que, tot i això, tenen moment magnètic (de fet el neutró no es considera realment elemental sinó format per tres quarks carregats).
| Partícula | Símbol | Valor [7](J/T) | Valor (magnetons) |
|---|---|---|---|
| Protó | |||
| Neutró | |||
| Electró | |||
| Muó |
Moment magnètic de l'electró
modificaEl moment (dipolar) magnètic d'un electró és:
siendo:
- , el magnetó de Bohr,
- [la teoria clàssica prediu que ; un gran èxit de l'equació de Dirac va ser la predicció que , que està molt a prop del valor exacte (que és lleugerament superior a dos; aquesta darrera correcció es deu als efectes quàntics del camp electromagnètic)].
- , la constant de Planck racionalitzada, i
- , l'espí de l'electró.
Moment magnètic dels electrons
modificaEls electrons i molts nuclis atòmics tenen moment magnètic, una explicació, que utilitza la mecànica quàntica i la relaciona amb el moment angular intrínsec de les partícules és a l'article moment dipolar magnètic de l'electró. Es tracta de moments magnètics que ocasionen l'efecte macroscòpic del magnetisme i d'altres fenòmens com la ressonància magnètica nuclear.
El moment magnètic de l'electró és:
on
- és el Magnetó de Bohr,
i
- = 2 en mecànica de Dirac, però és una mica més gran degut als efectes de l'electrodinàmica quàntica.
També és important ressaltar que és una constant negativa multiplicada per l'spin, això significa que el moment magnètic és antiparal·lel respecte al moment angular del spin. Això es pot comprendre amb la següent imatge clàssica: si imaginem que el moment angular del spin el crea la massa de l'electró girant entorn d'un eix, el corrent elèctric que crearà aquesta rotació girarà en direcció oposada a causa de la càrrega negativa de l'electró; una espira de corrent com aquesta produeix un moment magnètic que és antiparal·lel respecte al moment angular de l'espín.
Moment magnètic del nucli
modifica- Vegeu també moment magnètic nuclear
El nucli atòmic és un sistema físic complex compost de nucleons, com ara els protons i neutrons. Entre les propietats quàntiques dels nucleons s'inclou l'espín. Com el moment electromagnètic del nucli depèn del spin individual dels nucleons, es pot considerar aquestes propietats com a mesures de moments nuclears, i de manera més específica, del moment magnètic dipolar.
El moment magnètic nuclear és molt sensible respecte de les contribucions individuals dels nucleons i una mesura o predicció del seu valor pot mostrar informació important sobre el contingut de la funció d'ona del nucli. Hi ha diversos models teòrics que prediuen el valor del moment magnètic dipolar i diferents tècniques experimentals intenten de mesurar-lo.
Models
modificaL?explicació clàssica preferida d?un moment magnètic ha canviat amb el temps. Abans de la dècada del 1930, els llibres de text explicaven el moment utilitzant càrregues puntuals magnètiques hipotètiques. Des de llavors, la majoria ho ha definit en termes de corrents amperians.[8] En els materials magnètics, la causa del moment magnètic són els estats de moment angular orbital i gir dels electrons, i varia depenent de si els àtoms en una regió estan alineats amb àtoms en un altre.
Model de pol magnètic
modificaLes fonts de moments magnètics en els materials es poden representar per pols en analogia amb electroestàtica. Això de vegades es coneix com el model de Gilbert.[9] En aquest model, un petit imant és modelat per un parell de monopols magnètics ficticis d'igual magnitud però polaritat magnètica oposada. Cada pol és la font de força magnètica que s'afebleix amb la distància. Atès que els pols magnètics sempre vénen en parells, les seves forces s'anul·len parcialment perquè mentre un pol tira, l'altre es repel·leix. Aquesta cancel·lació és més gran quan els pols estan a prop un de l'altre, és a dir, quan la barra magnètica és curta. La força magnètica produïda per un imant de barra, en un punt donat de l'espai, depèn, per tant, de dos factors: la força p dels seus pols (“força del pol magnètic”), i el vector separant-los. El moment dipolar magnètic m està relacionat amb els pols ficticis com[8]
Apunta a la direcció del pol sud al pol nord. L'analogia amb els dipols elèctrics no s'ha de portar gaire lluny perquè els dipols magnètics estan associats amb el moment angular (vegeu relació amb el moment angular). No obstant això, els pols magnètics són molt útils per als càlculs de magnetoestàtica, particularment en aplicacions a ferromagnets.[8] Els practicants que usen l'enfocament del pol magnètic generalment representen el camp magnètic pel camp irrotacional] H, en analogia amb el camp elèctric E.
Referències
modifica- ↑ «moment magnètic». Gran Enciclopèdia Catalana. [Consulta: 13 novembre 2022].
- ↑ «moment». Diccionari General de la Llengua Catalana. Institut d'Estudis Catalans. [Consulta: 13 novembre 2022].
- ↑ «Unidades magnéticas». IEEE Magnetics. Arxivat de l'original el 2017-05-08. [Consulta: 19 febrer 2016].
- ↑ Mohr, Peter J.; Newell, David B.; Taylor, Barry N. «CODATA Valores recomendados de las constantes físicas fundamentales: 2014». Reviews of Modern Physics, vol. 88, 3, 21-07-2015, pàg. 035009. arXiv: 1507.07956. Bibcode: 2016RvMP...88c5009M. DOI: 10.1103/RevModPhys.88.035009.
- ↑ The International System of Units (9th ed.), International Bureau of Weights and Measures, Dec 2022, ISBN 978-92-822-2272-0, <https://www.bipm.org/documents/20126/41483022/SI-Brochure-9-EN.pdf>
- ↑ «K&J Magnetics - Glossary». www.kjmagnetics.com.
- ↑ «CODATA values of Atomic and Nuclear Constants». The NIST Reference on Constants, Units, and Uncertainty. [Consulta: 14 novembre 2014].
- ↑ 8,0 8,1 8,2 Brown, William Fuller, Jr.. Magnetostatic Principles in Ferromagnetism. North-Holland, 1962.
- ↑ Griffiths, David J. Introduction to Electrodynamics. 3rd. Prentice Hall, 1999, p. 258. ISBN 978-0-13-805326-0. OCLC 40251748.



