Reacció (física)
En enginyeria estructural i enginyeria mecànica, una reacció és una força de subjecció d'un element resistent a terra o un altre element de grans dimensions que serveix de suport a l'element resistent. En sentit general a vegades es parla de moments d'encastament o moments reacció, en el cas d'enllaços que a més impedeixen el gir d'algunes seccions d'unió.
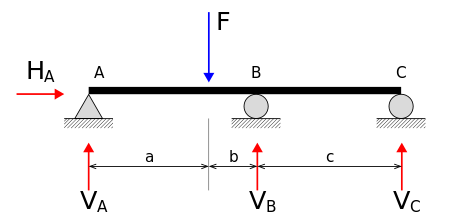
Mètodes de càlcul de reaccions
modificaEl càlcul de reaccions implica calcular un nombre de paràmetres (forces o moments) és superior o igual al nombre de graus de llibertat eliminen les unions amb l'exterior d'una estructura o mecanisme.
Si el nombre de reaccions incògnita és inferior a tres l'element resistent és considerat un mecanisme i requereix en general un càlcul dinàmic per determinar completament les reaccions. Si el nombre de reaccions incògnita és igual a tres, es tracta d'una estructura externament isostàtica i les equacions de l'estàtica són suficients per determinar les reaccions. Quan el nombre de reaccions és superior a tres, es tracta d'una estructura hiperestàtica i és necessari considerar la seva rigidesa per poder determinar completament les reaccions. En aquest últim cas existeixen diversos mètodes per determinar-les:
Condició d'equilibri
modificaDonat un sòlid una condició necessària perquè aquest sòlid estigui en equilibri mecànic és que la suma de reaccions i el moment resultant d'aquestes reaccions sigui zero:
Si el sòlid és indeformable la condició, a més de necessària, és suficient. Tanmateix, per certs sòlids deformables, la condició que la suma de força i moments s'anul·li pot no ser suficient. En aquell últim cas a més cal satisfer localment les equacions diferencials d'equilibri:
On:
- denoten les components del tensor de tensions.
- és la força per unitat de volum actuant a cada punt del sòlid.
Les condicions anteriors també són aplicables a un fluid i per la majoria de fluids admeten les equacions anteriors són equivalents a una forma més simple.
Referències
modifica- Marion i Thornton, Classical Dynamics of Particles and Systems. 4a edició, Harcourt Brace & Company (1995). (anglès)