Corba de Lamé

Una corba de Lamé és una figura geomètrica definida en el sistema de coordenades cartesianes com el conjunt de tots els punts (x, y) amb

Corba de Lamé amb n = 1/2, a = b = 1

Corba de Lamé amb n = 3/2, a = b = 1

Corba de Lamé amb n = 4, a = b = 1

$\left|{\frac {x}{a}}\right|^{n}\!+\left|{\frac {y}{b}}\right|^{n}\!=1$

on n, a i b són nombres positius.

Aquesta fórmula defineix una corba tancada continguda en el rectangle −a ≤ x ≤ +a i −b ≤ y ≤ +b. Els paràmetres a i b s'anomenen el semidiàmetres de la corba.

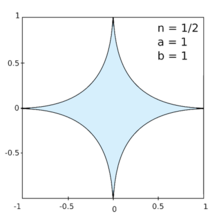
Quan n està entre 0 i 1, la corba de Lamé s'assembla a una estrella de quatre braços amb costats curvilinis cap a dins. Per n = 1/2, en particular, els costats són arcs de paràboles.

Quan n és 1 la corba és un diamant amb cantonades (±a, 0) i (0, ±b). Quan n està entre 1 i 2, s'assembla a un diamant amb aquelles mateixes cantonades però amb costats convexos (curvilini cap enfora). La curvatura augmenta sense límit en aproximar-se a les cantonades.

Quan n és 2, la corba és una el·lipse corrent (en particular, una circumferència si a = b). Quan n és més gran que 2, s'assembla superficialment a un rectangle amb cantonades axamfranades. La curvatura és zero en els punts (±a, 0) i (0, ±b).

Si n < 2, la figura també s'anomena una hipoel·lipse; si n > 2, un hyperellipse.

Quan n ≥ 1 i a = b, la corba de Lamé és el límit d'una bola de R² en la n-norma.

Els punts extrems de la corba de Lamé són (±a, 0) i (0; ±b), i les seves quatre "cantonades" són (±sa, ±sb), on $s=2^{-1/n}$ (a vegades anomenat el "superness").

Propietats algebraiques

Quan n és un nombre racional diferent de zero p / q (en fracció ireductible), llavors la corba de Lamé és una corba algebraica plana. Per a valors positius de n l'ordre és pq; per a valors negatius de n l'ordre és 2 pq. En particular, quan a i b són els dos u i n és un enter parell, llavors és una corba de Fermat de grau n. En aquest cas és no singular, però en general serà singular. Si el numerador no és parell, llavors la corba és el resultat d'enganxar porcions de la mateixa corba algebraica en orientacions diferents.

Animació

Per exemple, si x ^4/3 + y ^4/3 = 1, llavors la corba és una corba algebraica del grau dotze i gènere tres, donada per l'equació implícita

$(x^{4}+y^{4})^{3}-3(x^{4}-3x^{2}y^{2}+y^{4})(x^{4}+3x^{2}y^{2}+y^{4})+3(x^{4}+y^{4})-1=0,\,\!$

o per les equacions paramètriques

$\left.{\begin{aligned}x\left(\theta \right)&=\pm a\cos ^{\frac {2}{n}}\theta \\y\left(\theta \right)&=\pm b\sin ^{\frac {2}{n}}\theta \end{aligned}}\right\}\qquad 0\leq \theta <{\frac {\pi }{2}}$

o

${\begin{aligned}x\left(\theta \right)&={|\cos \theta |}^{\frac {2}{n}}\cdot a\operatorname {sgn}(\cos \theta )\\y\left(\theta \right)&={|\sin \theta |}^{\frac {2}{n}}\cdot b\operatorname {sgn}(\sin \theta ).\end{aligned}}$

L'àrea dins de la corba de Lamé es pot expressar en termes de la funció Gamma, Γ(x), com

$\mathrm {Area} =4ab{\frac {\left(\Gamma \left(1+{\tfrac {1}{n}}\right)\right)^{2}}{\Gamma \left(1+{\tfrac {2}{n}}\right)}}.$

Generalitzacions

Exemple de la corba de Lamé generalitzada amb m ≠ n.

La corba de Lamé es generalitza més com:

$\left|{\frac {x}{a}}\right|^{m}+\left|{\frac {y}{b}}\right|^{n}=1;\qquad m,n>0.$

o

${\begin{aligned}x\left(\theta \right)&={|\cos \theta |}^{\frac {2}{m}}\cdot a\operatorname {sgn}(\cos \theta )\\y\left(\theta \right)&={|\sin \theta |}^{\frac {2}{n}}\cdot b\operatorname {sgn}(\sin \theta ).\end{aligned}}$

Història

La notació cartesiana general de la forma ve del matemàtic francès Gabriel Lamé (1795–;1870) que va generalitzar l'equació de l'el·lipse.

Encara que se li atribueix sovint la seva invenció, el poeta danès i científic Piet Hein (1905-1996) no va descobrir la corba de Lamé. El 1959, planificadors de ciutat a Estocolm, Suècia varen anunciar un concurs de disseny per a una intersecció giratòria a la seva plaça de la ciutat Sergels torg. La proposta que va guanyar de Piet Hein es basava en una corba de Lamé amb n = 2.5 i a /b = 6/5. Tal com ho explicava:

l'Home és l'animal que dibuixa línies amb què ell mateix llavors ensopega. En tot l'esquema de la civilització hi ha hagut dues tendències, una cap a rectes i patrons rectangulars i una cap a circumferències. Hi ha raons, mecàniques i psicològiques, per a les dues tendències. Les coses fetes de rectes encaixen bé juntes i estalvien espai. I ens podem moure fàcilment — físicament o mentalment — al voltant de coses fetes amb al voltant de circumferències. Però som en una camisa de força, havent d'acceptar-ne un o l'altre, quan sovint una forma intermèdia seria millor. Dibuixar alguna cosa a mà alçada — com la rotonda que provaren a Estocolm — no ho resoldrà. No ho soluciona, no és clarament com una circumferència o un quadrat. No se sap què és. No és estèticament satisfactori. La corba de Lamé resol el problema. No és ni circumferència ni rectangular, sinó quelcom enmig. Ara està resolt, és — definitiu; té una unitat.

Sergels Torg es va completar el 1967. Mentrestant Piet Hein passava en utilitzar la corba de Lamé en altres artefactes, com ara llits, plats, taules, etc. Girant una corba de Lamé al voltant de l'eix més llarg, va crear el superou, un sòlid amb forma d'ou que es pot quedar vertical en una superfície plana, i era comercialitzat com a joguina.

El 1968, quan els negociadors a París per a la Guerra del Vietnam no es podien posar d'acord en la forma de la taula de negociacions, Balinski, Kieron Underwood i Holt en una carta al The New York Times suggerien una taula en forma de corba de Lamé. La corba de Lamé es va fer servir a la forma de l'Estadi Olimpic Azteca de 1968, a Ciutat de Mèxic.

Waldo Tobler va desenvolupar una projecció cartogràfica, la Projecció hiperelíptica de Tobler, publicada el 1973, en la qual els meridians són arcs de corbes de Lamé.

La tipografia d'Hermann Zapf Melior, publicada el 1952, fa servir corbes de Lamé per a lletres com la o. Molts llocs web diuen que Zapf de fet va dibuixar les formes de Melior a mà sense saber el concepte matemàtic de la corba de Lamé, i només més tard Piet Hein assenyalava a Zapf que les seves corbes eren extremadament similars a l'estructura matemàtica, però aquests llocs web no citen cap font primària d'aquesta història. Trenta anys més tard Donald Knuth construïa a la seva família de tipus Computer Modern la possibilitat de triar entre el·lipses veritables i corbes de Lamé (les dues aproximades per splines cúbics).

Al logo dels Pittsburgh Steelers es fan servir tres corbes de Lamé connectades.

Vegeu també

• Astroide, la corba de Lamé amb n = 2/3 i a = b és una hipocicloide amb quatre cúspides.
• Corba deltoide la hipocicloide de tres cúspides.

Referències

• Barr, Alan H. Geometric Modeling and Fluid Dynamic Analysis of Swimming Spermatozoa. Rensselaer Polytechnic Institute, 1983.  (Utilitzant la dissertació de Ph.D superel·lipsoides)
• Barr, Alan H. «Rigid Physically Based Superquadrics». A: Kirk, David. Graphics Gems III. Academic Press, 1992, p. 137–159 (code: 472–477). ISBN 978-0-12-409672-1. 
• Gielis, Johan. Inventing the Circle: The Geometry of Nature. Antwerp: Geniaal Press, 2003. ISBN 978-90-807756-1-9. 
• Sokolov, D. D.. «Lamé curve». A: Springer Encyclopaedia of Mathematics, 2001. 

Enllaços externs

• Superellipse Calculator & Template Generator Arxivat 2016-02-02 a Wayback Machine.
• Superellipse (MathWorld)
• Lamé's Super Ellipse (Java-Applet) Arxivat 2009-02-27 a Wayback Machine.
• Super Ellipsoid (Java-Applet) Arxivat 2005-05-24 a Wayback Machine.
• Johan Gielis' Arxivat 2009-12-14 a Wayback Machine. and Bert Beirinckx' Arxivat 2007-12-06 a Wayback Machine. "Superformula".