Diagrama de Feynman
En teoria quàntica de camps, un diagrama de Feynman representa gràficament un procés de col·lisió o de desintegració de partícules, i fou inventat pel físic estatunidenc Richard Feynman per a facilitar els càlculs teòrics en física de partícules. El problema de calcular seccions eficaces de col·lisió en física de partícules consisteix en sumar sobre les amplituds de tots els canals intermedis possibles, amb un mètode conegut com a expansió pertorbativa. Tots els processos possibles que porten d'un estat inicial donat (amb partícules a i b) a un estat final donat (amb partícules c i d) es poden representar per diagrames de Feynman, que són molt més fàcils de representar mentalment que amb els termes matemàtics corresponents dels càlculs subjacents. Feynman va mostrar com calcular les amplituds teòriques associades a un diagrama donat tot usant les anomenades regles de Feynman, que es poden derivar a partir del Lagrangià de les interaccions del procés de col·lisió o desintegració subjacent. Cada línia interna correspon a un factor del propagador de la partícula virtual corresponent; cada vèrtex on les línies s'uneixen dona un factor proporcional a l'acoblament de la interacció corresponent, i les línies entrants i sortints afegeixen restriccions en l'energia, el moment i l'espín de les partícules interactuants. La probabilitat de cada resultat llavors és obtinguda sumant sobre totes aquestes possibilitats al quadrat. Aquesta tècnica es directament lligada a la formulació integral funcional de la mecànica quàntica, també inventada per Feynman.
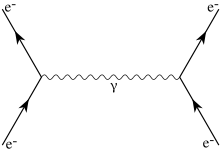
A més del seu valor com a tècnica matemàtica, els diagrames de Feynman proporcionen una bona intuïció física de la naturalesa de les interaccions de les partícules. No obstant, l'ús ingenu d'aquests càlculs produeix sovint diagrames amb amplituds infinites quan, per exemple, les auto-interaccions de les partícules han estat ignorades erròniament. La tècnica de la renormalització, iniciada per Feynman, Schwinger, i Tomonaga, compensa aquest efecte i elimina els termes infinits molestos. Després la renormalització, els càlculs de diagrames de Feynman coincideixen amb els resultats experimentals amb una exactitud altíssima. El diagrama de Feynman i els mètodes de la integral de trajectòries també s'utilitzen en la mecànica estadística.
Murray Gell-Mann es va referir sempre als diagrames de Feynman com a diagrames de Stückelberg, pel nom del físic suís, Ernst Stueckelberg, que va idear una notació semblant.
Interpretació modifica
Els diagrames de Feynman són realment una manera gràfica de no perdre de vista els índexs de DeWitt com fa la notació gràfica de Penrose per als índexs en àlgebra multilineal. Hi ha diversos diversos tipus per als índexs, un per a cada camp quàntic (aquest depèn de com s'agrupen els camps, per exemple, si el camp del quark "up" i el camp del quark "down" es tracten com a camps diferents, hi ha diversos tipus assignat a tots dos, però si es tracten com a un sol camp de diversos components amb "sabors", llavors seria només un tipus), les vores (és a dir els propagadors) són tensors de rang (2,0) en la notació DeWitt (és a dir amb dos índexs contravariant i cap covariant), mentre que els vèrtexs de grau n són tensors covariant de rang n que són totalment simètrics per a tots els índexs bosònics del mateix tipus i totalment antisimètrics per a tots els índexs fermiònics del mateix tipus. La contracció d'un propagador amb un tensor covariant de rang n és indicat per una vora incident a un vèrtex (no hi ha ambigüitat amb quin índex contraure perquè els vèrtexs corresponen als tensors totalment simètrics). Els vèrtexs externs corresponen als índexs contravariants no contrets.
Cada diagrama de Feynman individual sovint no té una interpretació física en si mateix. És només la suma infinita de tots els diagrames de Feynman possibles que dona resultats físics. Malauradament, aquesta suma infinita és només assimptòticament convergent.
Vegeu també modifica
| A Wikimedia Commons hi ha contingut multimèdia relatiu a: Diagrama de Feynman |