Ecologia teòrica
L'ecologia teòrica és una disciplina científica dedicada a estudiar els sistemes ecològics fent servir mètodes teòrics com els models conceptuals simples, models matemàtics, simulació per ordinador i anàlisi de dades avançats. Els models milloren la comprensió del món natural revelant com sovint la dinàmica de les poblacions de les espècies està basada en processos i condicions biològiques fonamentals. A més aquest camp científic intenta unificar un rang divers d'observacions empíriques assumint que els processos mecànics comuns generen fenòmens observables a través de les espècies i els ambients ecològics. Els ecoòlegs teòrics són capaços de descobrir nous aspectes no intuïtius sobre els processos naturals.
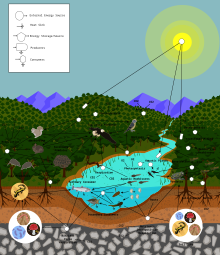
Aquest camp científic és ampli i inclou fonaments en la matemàtica aplicada, la ciència informàtica, la biologia, la física estadística, la genètica, la química, l'evolució i la biologia de la conservació. L'ecologia teòrica intenta explicar un rang divers de fenòmens com el creixement de les poblacion i la dinàmica de les zones pesqueres, la competència, la teoria de l'evolució, epidemiologia, el comportament animal i la dinàmica de grups, les xarxes alimentàries i els efectes del canvi climàtic.
Models
modificaCom en la majoria d'altres ciències els models matemàtics formen el fonament de l'ecologia teòrica.
- Models fenomenològics: des de patrons observats en les dades.[1]
- Models mecanicistes, amb funcions i distribucions basades en raonaments teòrics sobre processos ecològics.[1]
Els models ecològics poden ser deterministes o estocàstics.[1]
La teoria de la bifurcació es fa servir per mostrar com petits canvis en valors dels paràmetres poden originar sortides molt importants.[2] El mapa logístic és un mapa polinomial que proporciona exemples de com pot sorgir comportaments caòtics a partir d'equacions no linears.[3]
Com que els sistemes ecològics són típicament no lineals sovint no poden sser resolts analíticament i per això cal usar altres tècniques.[4]
Referències
modifica- ↑ 1,0 1,1 1,2 Bolker BM (2008) Ecological models and data in R Princeton University Press, pages 6–9. ISBN 9780691125220
- ↑ Ma T and Wang S (2005) Bifurcation theory and applications World Scientific. ISBN 9789812562876
- ↑ May, Robert. Theoretical Ecology: Principles and Applications. Blackwell Scientific Publishers, 1976. ISBN 0-632-00768-0.
- ↑ Supriatna AK (1998) Optimal harvesting theory for predator-prey metapopulations University of Adelaide, Department of Applied Mathematics.
Vegeu també
modificaBibliografia
modifica- El text clàssic és Theoretical Ecology: Principles and Applications, per Angela McLean i Robert May. L'edició de 2007 és d'Oxford University Press. ISBN 9780199209989.