Distribució de Cantor
La distribució Cantor és una probabilitat sobre els nombres reals, concentrada en el conjunt de Cantor, que té per funció de distribució la funció de Cantor.
Funció de distribució de probabilitat 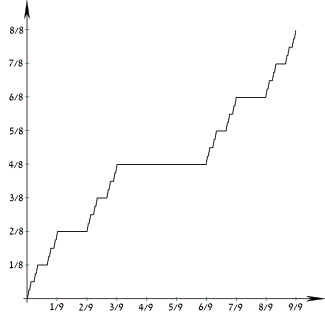 | |
| Tipus | Distribució singular i distribució de probabilitat contínua |
|---|---|
| Epònim | Georg Cantor |
| Paràmetres | none |
| Suport | Conjunt de Cantor |
| Esperança matemàtica | 1/2 |
| Mediana | en qualsevol lloc dins de [1/3, 2/3] |
| Moda | n/a |
| Variància | 1/8 |
| Coeficient de simetria | 0 |
| Curtosi | −8/5 |
| FC | |
Com que la funció de Cantor és contínua però no absolutament contínua, la distribució de Cantor no té part absolutament contínua respecte la mesura de Lebesgue (no té densitat) ni té part discreta; és un exemple de distribució singular.
En tot aquest article, designarà una variable aleatòria amb distribució de Cantor i el conjunt de Cantor.
Definició
modificaLa funció de Cantor és una funció no decreixent, contínua i amb i . Podem estendre-la a una funció definida en tot (utilitzem la mateixa lletra) posant si , i si . Aleshores és una funció de distribució, i per tant, determina una probabilitat a . Una variable aleatòria que tingui aquesta funció de distribució es diu que té (o segueix) una distribució de Cantor . Atès que és contínua, tindrem que per a qualsevol punt
Per tindrem
Atès que la funció de Cantor compleix , per a tot , on és el conjunt de Cantor, que té mesura de Lebesgue zero, es dedueix que a distribució de Cantor no té densitat,[1] és a dir, no existeix cap funció tal que
Suport de la distribució de Cantor
modificaEl suport de la distribució de Cantor és el conjunt de Cantor, que designarem per . És a dir, si és una variable aleatòria amb distribució de Cantor, aleshores . De fet, és el suport tancat de la distribució de Cantor: és el conjunt tancat més petit que té probabilitat 1.
Atès que el conjunt té mesura de Lebesgue zero, la distribució de Cantor és un exemple de distribució singular respecte la mesura de Lebesgue[2]
Caracterització de la distribució de Cantor
modificaRecordem que el conjunt de Cantor és la intersecció
Propietat. La distribució de Cantor és l'única distribució de probabilitat [3] tal que per qualsevol ,
Simetria de la distribució de Cantor
modificaDel fet que el gràfic de la funció de Cantor és simètric respecte el punt (1/2, 1/2) es dedueix que la distribució de Cantor és simètrica respecte del punt 1/2, o equivalentment, que si té una distribució de Cantor, llavors també.
Autosemblança de la distribució de Cantor
modificaAquesta propietat reposa en el caràcter fractal del conjunt . Diu que si seleccionem a l'atzar un dels intervals que formen , i prenem allí un punt d'acord amb la distribució de Cantor, tornem a obtenir la distribució de Cantor. En fórmules: siguin dues variables aleatòries independents, ambdues amb distribució de Cantor, i definim la variable aleatòria per:
independent de ; quan , elegim i quan elegim :
Moments
modificaAtès que , tenim que , d'on té moments de tots els ordres. De fet, la distribució de Cantor està determinada pels seus moments [6]
Esperança
modificaDel fet que i tenen ambdues distribucions de Cantor, es dedueix que
Moment de 2n ordre i variància
modificaDe la propietat d'autosemblança tenim
D'aquí s'obté:
Fórmula de recurrència pels moments
modificaUtilitzant la mateixa tècnica que a l'apartat anterior es pot trobar una fórmula de recurrència per als moments.[4] Escrivim
Llavors,
Expressió explicita dels moments
modificaLad and Taylor [4] donen la següent expressió pel moment d'ordre :
on B2n és el segon nombre de Bernoulli, i llavors expressant els moments com a funcions dels cumulants.
Funció característica
modificaUtilitzant també la propietat d'autosemblança es pot calcular la funció característica de la distribució de Cantor:[7]
La distribució de Cantor com a límit d'una passejada aleatòria
modificaConsiderem una successió de variables aleatòries independents i totes amb la següent distribució:
Definim la sèrie
Calculant la funció característica de es veu que té distribució de Cantor.[8]
Bibliografia
modifica- Falconer, K. J.. Geometry of Fractal Sets. Cambridge & New York: Cambridge Univ Press, 1985.
- Hu, Tian-You; Lau, Ka Sing. Fourier Asymptotics of Cantor Type Measures at Infinity. 130, 2002, p. 2711–2717.
- Knill, O. Probability Theory & Stochastic Processes. India: Overseas Press, 2006.
- Mandelbrot, B. The Fractal Geometry of Nature. San Francisco, CA: WH Freeman & Co., 1982.
- Mattilla, P. Geometry of Sets in Euclidean Spaces. San Francisco: Cambridge University Press, 1995.
- Saks, Stanislaw. Theory of the Integral. Warsaw: PAN, 1933. (Reprinted by Dover Publications, Mineola, NY.
Enllaços externs
modifica- Morrison, Kent. «Random Walks with Decreasing Steps». Department of Mathematics, California Polytechnic State University, 23-07-1998. Arxivat de l'original el 2015-12-02. [Consulta: 16 febrer 2007].
- Utzet, Frederic. «Una passejada aletòria pel conjunt de Cantor». Department de matemátiques, Universitat Autònoma de Barcelona, Materials Matemàtics, vol. 2020, no. 3, pp. 35, 2020.
Referències
modifica- ↑ 1,0 1,1 Loeve, Michel.. Teoría de la probabilidad. Madrid: Tecnos, D.L. 1976, p. 177. ISBN 84-309-0663-0.
- ↑ Loeve, Michel.. Teoría de la probabilidad. Madrid: Tecnos, D.L. 1976, p. 132. ISBN 84-309-0663-0.
- ↑ Mattila, Pertti,. Fourier analysis and Hausdorff dimension, p. 108. ISBN 978-1-107-10735-9.
- ↑ 4,0 4,1 4,2 Lad, F. R. and Taylor, F. C. R. «The moments of the Cantor distribuction». Stat. Prob. Let., Vol. 13, num. 4 (1992), pp. 307-310.
- ↑ Haro Provinciale, Àlex «Fractalitat, determinisme i caos en el conjunt de Cantor». Butlletí de la Societat Catalana de Matemàtiques, 27, 2012, pàg. 161–175. DOI: 10.2436/20.2002.01.44. ISSN: 2013-9829.
- ↑ Feller, William. Introducción a la teoría de las probabilidades y sus aplicaciones, Vol. II. 2a. edición. México: Editorial Limusa, 1978, p. Cap. 7, sec. 3.
- ↑ Dovgoshey, O., Martio, O., Ryazanov, V., Vuorinen, M. «The Cantor function». Expo. Math., Vol. 34 (2006), pp. 1-37.
- ↑ Billingsley, Patrick.. Probability and measure. 2a edició. Nova York: Wiley, 1986, p. 437. ISBN 0-471-80478-9.


