Teoria de cordes
La teoria de cordes és una proposta de descripció quàntica unificada de totes les interaccions, incloent-hi la gravetat, que considera que els constituents fonamentals de la matèria no són partícules puntuals sinó objectes unidimensionals (cordes).[1]

- Matèria.
- Estructura molecular.
- Àtoms.
- Electrons.
- Quarks (protons i neutrons).
- cordes.
La idea bàsica és que els components fonamentals del món físic són cordes d'una longitud de l'ordre de la longitud de Planck (10-35 m) que vibren a freqüències de ressonància. La tensió que haurien de tenir aquestes cordes (8,9·1042 N) és al voltant de 1041 vegades la tensió d'una corda de piano habitual (735 N). Per exemple, la teoria prediu que el gravitó (la proposada partícula transmissora de la força gravitacional) és una corda amb amplitud zero. Una altra idea clau proporcionada per la teoria és que no hi ha cap diferència perceptible entre cordes que es caragolen al voltant de dimensions més petites que les seves i les que es mouen en dimensions més grans (és a dir, els efectes en una dimensió de magnitud R igualen els de magnitud 1/R).
La teoria de supercordes és una versió de la teoria de cordes estàndard que inclou els fermions (cosa que l'estàndard no feia) i incorpora la supersimetria (una simetria de les partícules fonamentals que relaciona bosons i fermions). Un aspecte destacable d'aquesta versió és que, per tal que la descripció de la natura sigui consistent, es necessita que l'espaitemps tingui 10 dimensions, en lloc de les 4 dimensions observades (tres d'espacials i una de temporal). Hom generalment suposa que, de les 10 dimensions, n'hi ha 6 que es troben caragolades (compactificades) en escales properes a la longitud de Planck, i per aquest motiu no es poden percebre.
Aquesta teoria o, més ben dit, teories (vegeu més endavant), és una solució possible al problema de la gravetat quàntica (és a dir, una descripció quàntica de la gravetat) i, a més de la gravetat, pot descriure de manera natural les altres forces de la natura (força electrofeble i força forta). Les teories de supercordes inclouen els fermions i incorporen la supersimetria. No se sap encara si la teoria és capaç de descriure un univers amb la quantitat precisa de forces i matèria que observem, ni quanta llibertat la teoria dona per escollir aquests detalls. La teoria de cordes (i menys les seves ampliacions, com la teoria M) encara no ha fet prediccions falsables que permetin comprovar-la experimentalment, encara que alguns aspectes especials de la teoria són accessibles a observacions i experiments.
5 teories de cordes diferents modifica
Inicialment, la teoria de cordes es referia a la teoria de cordes bosònica (de 26 dimensions i que només inclou bosons), creada durant la dècada de 1960. Actualment, però, el terme s'aplica a qualsevol de les 5 teories de cordes que inclouen fermions i supersimetria (les supercordes, de 10 dimensions). Com a resultat dels treballs en la teoria de cordes, cap als anys 1990, semblava clar que hi havia 5 versions diferents de la teoria de cordes (o supercordes) consistents, però aparentment incompatibles entre si. Les 5 teories difereixen en el tipus de cordes que permeten i en com implementen la supersimetria. Són les següents:
- Tipus I: les cordes no tenen orientació (qualsevol de les dues orientacions és equivalent) i considera cordes tancades i obertes.
- Tipus II A: presenta la màxima supersimetria (32 supercàrregues) en deu dimensions. Les cordes són tancades i orientades i presenta simetria quiral (esquerra-dreta).
- Tipus II B: igual que l'anterior, però sense simetria quiral.
- Heteròtica SO(32): com que les excitacions de les cordes levògires i dextrògires són quasi independents, es pot construir una teoria en què les excitacions levògires "creguin" ser en una corda bosònica de 26 dimensions i les dextrògires en una supercorda de 10 dimensions. Les 16 dimensions de diferència es poden compactificar i hi ha dues possibilitats per a fer-ho: l'una dona lloc al SO(32). Les cordes són tancades.
- Heteròtica E₈×E₈: l'altra possibilitat de compactificar les 16 dimensions de diferència entre excitacions levògires i dextrògires. Les cordes són tancades.
Tot i que, per a entendre els detalls d'aquestes teories, cal un nivell considerable de coneixements matemàtics, algunes propietats es poden entendre de manera intuïtiva. Per exemple, les cordes tenen tensió (de manera semblant a les cordes normals del món macroscòpic) i aquesta tensió n'és un paràmetre fonamental i està molt relacionada amb la grandària de la corda: si es considera una corda tancada, com més tensió tingui més petit serà el llaç que forma.
El 1995, Edward Witten i d'altres indicaren que, possiblement, la teoria de cordes és, de fet, el límit d'una teoria més general -i en bona part per desenvolupar- d'11 dimensions, anomenada temptativament teoria M. La teoria de cordes seria un límit particular de la teoria M. En la teoria de cordes, es troben no solament cordes sinó també altres objectes no pertorbatius, com ara branes (superfícies de dimensions diverses). La proposta de Witten va desfermar una allau de recerca coneguda com la segona revolució de supercordes.[2]
Vibració de les cordes modifica
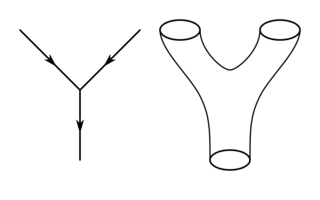
Segons la teoria de cordes, aquests components microscòpics estan constantment en vibració. Aquestes vibracions són diferents en cada corda i aporta a les partícules característiques molt destacades, com per exemple la seva massa. Una corda que vibra amb més energia serà més pesant que no pas una de més reposada (encara que també vibri), ja que traduïm que més energia és igual a un augment de la massa.
Èxits i problemes de la teoria de cordes modifica
Alguns dels èxits de la teoria de cordes són:
- Donar una descripció pertorbativa de la gravetat quàntica, unificada amb les altres interaccions.
- Ser una teoria finita, és a dir, no tenir els infinits que apareixen en la teoria quàntica de camps.
- Donar una descripció microscòpica de l'entropia d'un cert tipus de forat negre.
Alguns dels problemes o reptes de la teoria de cordes són:
- La manca de prediccions susceptibles de falsar. Els resultats de la teoria de cordes es refereixen a les escales de Planck, completament inaccessibles experimentalment avui dia i, per tant, no es poden contrastar en absolut. Hom ha arribat a argumentar que la teoria de cordes no fa cap mena de prediccions i que, per tant, no es pot considerar una teoria científica.
- Manca d'una explicació convincent de per què no s'observen les dimensions que superen les 4 conegudes.
- Manca d'una explicació de per què no s'observa la supersimetria en la natura.
- Manca d'una descripció no pertorbativa de la teoria de cordes, anàloga a la de la relativitat general.
Referències modifica
- ↑ Termcat. «Teoria de cordes». Diccionari de física. [Consulta: 5 desembre 2021].
- ↑ Duff, Michael «The theory formerly known as strings» (en anglès). Scientific American, 278, 2, 1998, pàg. 64–9. Bibcode: 1998SciAm.278b..64D. DOI: 10.1038/scientificamerican0298-64.
Vegeu també modifica
| A Wikimedia Commons hi ha contingut multimèdia relatiu a: Teoria de cordes |