Braquistòcrona

En física i matemàtiques, una corba braquistòcrona (del grec βράχιστος χρόνος (brákhistos khrónos); «temps més curt»), o «corba de descens més ràpid», és la que es troba en el pla entre un punt A i un punt inferior B, on B no és directament sota A, sobre la qual una bola llisca sense fricció sota la influència d'un camp gravitatori uniforme fins a un punt final determinat en el temps més curt. El problema va ser plantejat per Johann Bernoulli el 1696.

• 
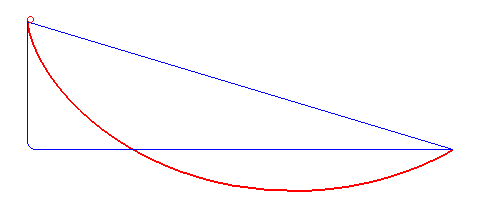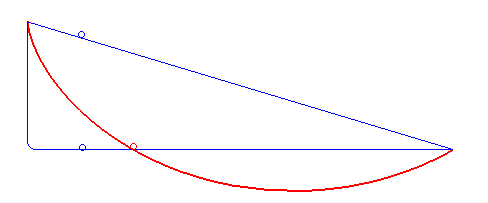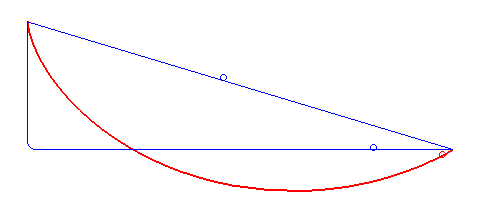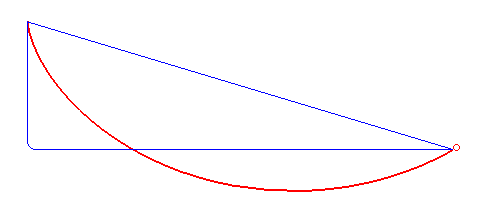
  La corba de descens més ràpid no és una línia recta o poligonal (blava) sinó una cicloide (vermell)

La corba braquistòcrona té la mateixa forma que la corba tautòcrona; tots dos són cicloides. Tanmateix, la porció de la cicloide utilitzada per a cadascun dels dos varia. Més concretament, la braquistòcrona pot utilitzar fins a una rotació completa de la cicloide (al límit quan A i B estan al mateix nivell), però sempre comença en una cúspide. En canvi, el problema tautòcrona només pot utilitzar fins a la primera meitat de rotació, i sempre acaba a l'horitzontal. El problema es pot resoldre mitjançant eines del càlcul de variacions i control òptim.

La corba és independent tant de la massa del cos de prova com de la força de gravetat local. Només s'escull un paràmetre perquè la corba s'ajusti al punt inicial A i al punt final B. Si al cos se li dóna una velocitat inicial en A, o si es té en compte la fricció, aleshores la corba que minimitza el temps difereix de la corba tautòcrona.

Història

Johann Bernoulli va plantejar el problema de la braquistòcrona als lectors d'Acta Eruditorum el juny de 1696.

Va dir:

«	Jo, Johann Bernoulli, em dirigeixo als matemàtics més brillants del món. Res és més atractiu per a les persones intel·ligents que un problema honest i desafiant, la possible solució del qual atorgarà fama i es mantindrà com un monument durador. Seguint l'exemple donat per Pascal, Fermat, etc., espero obtenir l'agraïment de tota la comunitat científica posant davant els millors matemàtics del nostre temps un problema que posarà a prova els seus mètodes i la força del seu intel·lecte. Si algú em comunica la solució del problema proposat, el declararé públicament digne de lloança.	»
— Johann Bernoulli

Bernoulli va escriure l'enunciat del problema de la següent manera:

«

Donats dos punts A i B en un pla vertical, quina és la corba traçada per un punt sobre el qual només actua la gravetat, que comença a A i arriba a B en el menor temps?

»

Johann i el seu germà Jakob Bernoulli van derivar la mateixa solució, però la derivació de Johann era incorrecta, i va intentar fer passar la solució de Jakob com la seva. Johann va publicar la solució a la revista el maig de l'any següent i va assenyalar que la solució és la mateixa corba que la corba tautòcrona de Huygens. Després de derivar l'equació diferencial per a la corba pel mètode que es mostra a continuació, va continuar demostrant que produeix un cicloide. Tanmateix, la seva prova es veu afectada per l'ús d'una sola constant en lloc de les tres constants, v_m, 2g i D, a continuació.

Bernoulli va permetre sis mesos per a les solucions, però no es va rebre cap durant aquest període. A petició de Leibniz, el temps es va prorrogar públicament durant un any i mig. A les 16.00 h. del 29 de gener de 1697, quan va arribar a casa des de la Royal Mint, Isaac Newton va trobar el repte en una carta de Johann Bernoulli. Newton es va quedar despert tota la nit per resoldre'l i va enviar la solució de forma anònima al següent missatge. En llegir la solució, Bernoulli va reconèixer immediatament el seu autor, exclamant que «reconec un lleó per la seva marca de les urpes». Aquesta història dóna una idea del poder de Newton, ja que Johann Bernoulli va trigar dues setmanes a resoldre'l. Newton també va escriure: «No m'encanta que els estrangers em burlin de coses matemàtiques...», i Newton ja havia resolt el problema de resistència mínima de Newton, que es considera el primer d'aquest tipus en càlcul de variacions.

Al final, cinc matemàtics van respondre amb solucions: Isaac Newton, Jakob Bernoulli, Gottfried Leibniz, Ehrenfried Walther von Tschirnhaus i Guillaume de l'Hôpital. Quatre de les solucions (excloent la de l'Hôpital) es van publicar a la mateixa edició de la revista que la de Johann Bernoulli. En el seu article, Jakob Bernoulli va donar una prova de la condició durant menys temps similar a la següent abans de demostrar que la seva solució és una cicloide. Segons l'estudiós newtonià Tom Whiteside, en un intent de superar al seu germà, Jakob Bernoulli va crear una versió més difícil del problema de la braquistòcrona. Per resoldre-ho, va desenvolupar nous mètodes que van ser refinats per Leonhard Euler en el que aquest últim va anomenar (el 1766) el càlcul de variacions. Joseph-Louis Lagrange va fer més treballs que van donar lloc al càlcul infinitesimal modern.

Abans, l'any 1638, Galileu havia intentat resoldre un problema similar per al camí del descens més ràpid d'un punt a una paret a les seves Discorsi e Dimostrazioni Matematiche Intorno a Due Nuove Scienze. Treu la conclusió que l'arc de cercle és més ràpid que qualsevol nombre de les seves cordes:

«

De l'anterior es pot inferir que el camí més ràpid de tots [lationem omnium velocissimam], d'un punt a un altre, no és el camí més curt, és a dir, una recta, sinó l'arc del cercle. (...) En conseqüència, com més s'acosta el polígon inscrit a una circumferència, més curt és el temps necessari per baixar d'A a C. El que s'ha demostrat per al quadrant és cert també per als arcs més petits; el raonament és el mateix.

»

Just després del Teorema 6 de Due Nuove Scienze, Galileu adverteix de possibles fal·làcies i de la necessitat d'una «ciència superior». En aquest diàleg Galileu repassa la seva pròpia obra. Galileu va estudiar la cicloide i li va donar nom, però la connexió entre aquesta i el seu problema va haver d'esperar als avenços de les matemàtiques.

• 
  Diagrames sobre la conjectura de Galileu

La conjectura de Galileu és que «El temps més curt de tots [per a un cos mòbil] serà el de la seva caiguda al llarg de l'arc ADB [d'un quart de cercle] i propietats similars s'han d'entendre com una retenció per a tots els arcs menors agafats cap amunt des del límit més baix B».

En conseqüència, a la figura 1, del Diàleg sobre els dos sistemes mundials principals, Galileu afirma que el cos lliscant al llarg de l'arc circular d'un quart de cercle, d'A a B, arribarà a B en menys temps que si prengués qualsevol altre camí d'A a B. De la mateixa manera, a la figura 2, des de qualsevol punt E de l'arc AB, afirma que el temps al llarg de l'arc menor EB serà menor que per a qualsevol altre camí d'E a B. De fet, el camí més ràpid d'A a B o d'E a B, la braquistòcrona, és un arc cicloïdal, que es mostra a la figura 3 per al camí d'E a B. Les dues corbes es superposen a la figura 4. Nota: la conjectura de Galileu té la tangent de la corba horitzontal al punt final, B, mentre que la braquistòcrona té la tangent vertical al punt inicial, E. Com a conseqüència, l'arc circular i l'arc cicloïdal de la figura 4 s'han de tallar en algun punt entre E i B.

La solució de Johann Bernoulli

Introducció

En una carta a L'Hôpital, (21/12/1696), Bernoulli va afirmar que quan es plantejava el problema de la corba de descens més ràpid, després de només dos dies va notar una curiosa afinitat o connexió amb un altre problema no menys notable que portava a un «mètode indirecte» de solució. Poc després va descobrir un «mètode directe».

El mètode directe

En una carta a Henri Basnage, conservada a la Biblioteca Pública de la Universitat de Basilea, datada el 30 de març de 1697, Johann Bernoulli va declarar que havia trobat dos mètodes (sempre anomenats «directe» i «indirecte») per demostrar que la braquistòcrona era la «cicloide comuna», també anomenada «ruleta». Seguint el consell de Leibniz, va incloure només el «mètode indirecte» a l'Acta Eruditorum Lipsidae de maig de 1697. Va escriure que això era en part perquè creia que era suficient per convèncer qualsevol que dubtés de la conclusió, en part perquè també va resoldre dos famosos problemes d'òptica que «el difunt senyor Huygens» havia plantejat en el seu tractat de la llum. En la mateixa carta va criticar a Newton per amagar el seu mètode.

A més del seu mètode indirecte, també va publicar les altres cinc respostes al problema que va rebre.

El «mètode directe» de Johann Bernoulli és històricament important com a prova que la braquistòcrona és el cicloide. El mètode consisteix a determinar la curvatura de la corba en cada punt. Totes les altres proves, inclosa la de Newton (que no es va revelar en aquell moment) es basen en trobar el gradient en cada punt.

El 1718, Bernoulli va explicar com va resoldre el problema de la braquistòcrona pel seu mètode directe.

Va explicar que no l'havia publicat el 1697, per raons que ja no s'aplicaven el 1718. Aquest article va ser ignorat en gran mesura fins al 1904, quan Constantin Carathéodory va apreciar per primera vegada la profunditat del mètode, que va afirmar que demostra que la cicloide és el única corba possible de baixada més ràpida. Segons ell, les altres solucions simplement implicaven que el temps de descens és estacionari per a la cicloide, però no necessàriament el mínim possible.

La solució analítica

Es considera que un cos llisca al llarg de qualsevol petit arc circular Ce entre els radis KC i Ke, amb el centre fix K. La primera etapa de la demostració consisteix a trobar l'arc circular particular, Mm, que el cos recorre en el temps mínim.

• 
  Mètode directe de la braquistòcrona de Bernoulli

La recta KNC talla AL en N, i la línia Kne la talla en n, i formen un petit angle CKe en K. Sigui NK = a, i defineixi un punt variable, C sobre KN estès. De tots els arcs circulars possibles Ce, cal trobar l'arc Mm, que requereix el temps mínim per lliscar entre els dos radis, KM i Km. Per trobar Mm, Bernoulli argumenta el següent:

Sigui MN = x. Defineixi m de manera que MD = mx, i n de manera que Mm = nx + na i assenyali que x és l'única variable i que m és finita i n és infinitament petita. El petit temps per viatjar per l'arc Mm és ${\frac {Mm}{MD^{\frac {1}{2}}}}={\frac {n(x+a)}{(mx)^{\frac {1}{2}}}}$, que ha de ser un mínim («un plus petit»). No explica que com que Mm és tan petita, es pot suposar que la velocitat al llarg d'ella és la velocitat a M, que és com l'arrel quadrada de MD, la distància vertical de M per sota de la línia horitzontal AL.

Es dedueix que, quan es diferencia això ha de donar

${\frac {(x-a)dx}{2x^{\frac {3}{2}}}}=0$ de manera que x = a.

Aquesta condició defineix la corba per la qual llisca el cos en el menor temps possible. Per a cada punt, M de la corba, el radi de curvatura, MK es talla en dues parts iguals pel seu eix AL. Aquesta propietat, que Bernoulli diu que era coneguda des de fa molt de temps, és exclusiva de la cicloide.

Finalment, considera el cas més general en què la velocitat és una funció arbitrària X(x), de manera que el temps a minimitzar és ${\frac {(x+a)}{X}}$.

Aleshores es converteix en la condició mínima

$X={\frac {(x+a)dX}{dx}}$

que ell escriu com:

$X=(x+a)\Delta x$

i que dóna MN (=x) en funció de NK (= a). A partir d'això, l'equació de la corba es podria obtenir a partir del càlcul integral, encara que no ho demostra.

La solució sintètica

A continuació, continua amb el que va anomenar la seva solució sintètica, que era una prova geomètrica clàssica, que només hi ha una sola corba que un cos pot lliscar cap avall en el temps mínim, i aquesta corba és la cicloide.

El motiu de la demostració sintètica, a la manera dels antics, és per convèncer el senyor de La Hire. Té poc temps per a la nostra nova anàlisi, descrivint-la com a fals.

Suposem que AMmB és la part de la cicloide que uneix A a B, on el cos llisca cap avall en el temps mínim. Sigui ICcJ part d'una corba diferent que uneix A a B, que pot estar més propera a AL que AMmB. Si l'arc Mm subtendeix l'angle MKm en el seu centre de curvatura, K, sigui Cc l'arc de IJ que subteneix el mateix angle. L'arc circular per C amb centre K és Ce. El punt D de AL està verticalment per sobre de M. Uneix K a D i el punt H és on CG talla KD, allargat si cal.

Fem que $\tau$ i t siguin els temps que el cos triga a caure al llarg de Mm i Ce, respectivament.

$\tau \propto {\frac {Mm}{MD^{\frac {1}{2}}}}$, $t\propto {\frac {Ce}{CG^{\frac {1}{2}}}}$,

Extenent CG fins al punt F on, $CF={\frac {CH^{2}}{MD}}$ i des de ${\frac {Mm}{Ce}}={\frac {MD}{CH}}$, se segueix que

${\frac {\tau }{t}}={\frac {Mm}{Ce}}.\left({\frac {CG}{MD}}\right)^{\frac {1}{2}}=\left({\frac {CG}{CF}}\right)^{\frac {1}{2}}$

Com que MN = NK, per a la cicloide:

$GH={\frac {MD.HD}{DK}}={\frac {MD.CM}{MK}}$, $CH={\frac {MD.CK}{MK}}={\frac {MD.(MK+CM)}{MK}}$, i $CG=CH+GH={\frac {MD.(MK+2CM)}{MK}}$

Si Ce està més a prop de K que de Mm, aleshores

$CH={\frac {MD.(MK-CM)}{MK}}$ and $CG=CH-GH={\frac {MD.(MK-2CM)}{MK}}$

En qualsevol cas,

$CF={\frac {CH^{2}}{MD}}>CG$, i se segueix que $\tau <t$

Si l'arc, Cc subtessant per l'angle infinitesimal MKm a IJ no és circular, ha de ser més gran que Ce, ja que Cec es converteix en un triangle rectangle en el límit quan l'angle MKm s'acosta a zero.

S'ha d'observar que Bernoulli demostra que CF > CG amb un argument semblant però diferent.

D'això conclou que un cos travessa la cicloide AMB en menys temps que qualsevol altra corba ACB.

Mètode indirecte

Segons el principi de Fermat, el camí real entre dos punts que pren un feix de llum és el que triga menys temps. El 1697 Johann Bernoulli va utilitzar aquest principi per derivar la corba braquistòcrona considerant la trajectòria d'un feix de llum en un medi on la velocitat de la llum augmenta seguint una acceleració vertical constant (la de la gravetat g).

Per la conservació de l'energia, la velocitat instantània d'un cos v després de caure una alçada y en un camp gravitatori uniforme ve donada per:

$v={\sqrt {2gy}}$,

La velocitat de moviment del cos al llarg d'una corba arbitrària no depèn del desplaçament horitzontal.

Bernoulli va assenyalar que la llei de refracció dóna una constant del moviment per a un feix de llum en un medi de densitat variable:

${\frac {\sin {\theta }}{v}}={\frac {1}{v}}{\frac {dx}{ds}}={\frac {1}{v_{m}}}$,

on v_m és la constant i 𝜃 representa l'angle de la trajectòria respecte a la vertical.

Les equacions anteriors porten a dues conclusions:

• Al principi, l'angle ha de ser zero quan la velocitat de les partícules és zero. Per tant, la corba braquistòcrona és tangent a la vertical a l'origen.
• La velocitat assoleix un valor màxim quan la trajectòria es fa horitzontal i l'angle θ = 90°.

Suposant per simplicitat que la partícula (o el feix) amb coordenades (x,y) s'allunya del punt (0,0) i assoleix la velocitat màxima després de caure una distància vertical D:

$v_{m}={\sqrt {2gD}}$.

La reordenació dels termes de la llei de la refracció i el quadrat dóna:

$v_{m}^{2}dx^{2}=v^{2}ds^{2}=v^{2}(dx^{2}+dy^{2})$

que es pot resoldre per a dx en termes de dy:

$dx={\frac {v\,dy}{\sqrt {v_{m}^{2}-v^{2}}}}$.

Substituint a partir de les expressions de v i v_m anteriors s'obté:

$dx={\sqrt {\frac {y}{D-y}}}\,dy\,,$

que és l'equació diferencial d'una cicloide invertida generada per un cercle de diàmetre D=2r, l'equació paramètrica del qual és:

${\begin{aligned}x&=r(\varphi -\sin \varphi )\\y&=r(1-\cos \varphi ).\end{aligned}}$

on φ és un paràmetre real, corresponent a l'angle pel qual ha girat el cercle rodant. Per a φ donat, el centre del cercle es troba a (x, y) = (rφ, r)

En el problema de la braquistòcrona, el moviment del cos ve donat per l'evolució temporal del paràmetre:

$\varphi (t)=\omega t\,,\omega ={\sqrt {\frac {g}{r}}}$

on t és el temps des de l'alliberament del cos des del punt (0,0).

La solució de Jakob Bernoulli

El germà de Johann, Jakob Bernoulli, va mostrar com es poden utilitzar els 2n diferencials per obtenir la condició durant el menor temps. Una versió modernitzada de la prova és la següent:

Si fem una desviació insignificant del camí de menys temps, aleshores, per al triangle diferencial format pel desplaçament al llarg del camí i els desplaçaments horitzontals i verticals,

$ds^{2}=dx^{2}+dy^{2}$.

En la diferenciació amb dy fix obtenim,

$2ds\ d^{2}s=2dx\ d^{2}x$.

I finalment reordenar els termes dóna,

${\frac {dx}{ds}}d^{2}x=d^{2}s=v\ d^{2}t$

on l'última part és el desplaçament per un canvi de temps donat per a les 2n diferencials. S'ha de considerar ara els canvis al llarg dels dos camins veïns de la figura següent per als quals la separació horitzontal entre camins al llarg de la línia central és d²x (la mateixa per als triangles diferencials superior i inferior). Al llarg dels camins antics i nous, les parts que es diferencien són,

$d^{2}t_{1}={\frac {1}{v_{1}}}{\frac {dx_{1}}{ds_{1}}}d^{2}x$

$d^{2}t_{2}={\frac {1}{v_{2}}}{\frac {dx_{2}}{ds_{2}}}d^{2}x$

Funció del camí

Pel camí de menys temps aquests temps són iguals, així que per la seva diferència obtenim,

$d^{2}t_{2}-d^{2}t_{1}=0={\bigg (}{\frac {1}{v_{2}}}{\frac {dx_{2}}{ds_{2}}}-{\frac {1}{v_{1}}}{\frac {dx_{1}}{ds_{1}}}{\bigg )}d^{2}x$

I la condició de menys temps és,

${\frac {1}{v_{2}}}{\frac {dx_{2}}{ds_{2}}}={\frac {1}{v_{1}}}{\frac {dx_{1}}{ds_{1}}}$

que concorda amb la suposició de Johann basada en la llei de la refracció.

La solució de Newton

Introducció

El juny de 1696, Johann Bernoulli va utilitzar les pàgines de l'Acta Eruditorum Lipsidae per plantejar un repte a la comunitat matemàtica internacional: «trobar la forma de la corba que uneix dos punts fixos de manera que una massa llisqui cap avall, sota la influència de només la gravetat, en el mínim temps». La solució s'havia de presentar inicialment en un termini de sis mesos. A proposta de Leibniz, Bernoulli va allargar el repte fins a Pasqua de 1697, mitjançant un text imprès anomenat «Programma», publicat a Groningen, als Països Baixos.

El Programa està datat el 1r de gener de 1697, al calendari gregorià. Va ser el 22 de desembre de 1696 al calendari julià, en ús a Gran Bretanya.

Segons la neboda de Newton, Catherine Conduitt, Newton es va assabentar del repte a les 4 de la tarda del 29 de gener i l'havia resolt a les 4 de la matinada del dia següent. La seva solució, comunicada a la Royal Society, està datada el 30 de gener. Aquesta solució, publicada posteriorment de manera anònima a Philosophical Transactions, és correcta però no indica el mètode pel qual Newton va arribar a la seva conclusió. Bernoulli, escrivint a Henri Basnage el març de 1697, va indicar que tot i que el seu autor, «per un excés de modèstia», no havia revelat el seu nom, encara que fins i tot pels escassos detalls proporcionats es podia reconèixer com l'obra de Newton, «com el lleó per la seva urpa» (en llatí, ex ungue Leonem).

D. T. Whiteside explica de manera característica l'origen de l'expressió llatina, originària del grec, amb un gran detall. La carta en francès té «ex ungue Leonem» precedit de la paraula francesa «comme» (com). La molt citada versió «tanquam ex ungue Leonem» es deu al llibre de David Brewster sobre la vida i les obres de Newton el 1855. La intenció de Bernoulli era simplement que pogués dir que la solució anònima era la de Newton, de la mateixa manera que era possible dir que un animal era un lleó donat la seva urpa. No pretenia suggerir que Bernoulli considerés que Newton era el lleó entre els matemàtics, tal com s'ha interpretat des de llavors.

John Wallis, que en aquell moment tenia 80 anys, s'havia assabentat del problema el setembre de 1696 del germà petit de Johann Bernoulli, Hieronymus, i va passar tres mesos intentant una solució abans de passar-ho al desembre a David Gregory, que tampoc no va poder resoldre'l. Després que Newton va presentar la seva solució, Gregory li va demanar els detalls i va prendre notes de la seva conversa. Es poden trobar a la Biblioteca de la Universitat d'Edimburg, manuscrit A $78^{1}$, del 7 de març de 1697. O Gregory no va entendre l'argument de Newton, o bé l'explicació de Newton va ser molt breu. Tanmateix, és possible, amb un alt grau de confiança, construir la demostració de Newton a partir de les notes de Gregory, per analogia amb el seu mètode per determinar el sòlid de resistència mínima (Principia, Llibre 2, Proposició 34, Escolis 2). Una descripció detallada de la seva solució d'aquest darrer problema s'inclou a l'esborrany d'una carta l'any 1694, també a David Gregory. A més del problema de la corba de temps mínim, hi va haver un segon problema que Newton també va resoldre al mateix temps. Ambdues solucions van aparèixer de manera anònima a Philosophical Transactions de la Royal Society, per al gener de 1697.

El problema de la braquistòcrona

La figura 1, mostra el diagrama de Gregori (excepte que la línia addicional IF no hi estigui, i Z, s'ha afegit el punt inicial). La corba ZVA és una cicloide i CHV és el seu cercle generador. Com que sembla que el cos es mou cap amunt d'e a E, cal suposar que un cos petit s'allibera de Z i llisca al llarg de la corba fins a A, sense fricció, sota l'acció de la gravetat.

• 
  Repte 1 de Bernoulli a Newton

S'ha de considerar un petit arc eE, que el cos està ascendint. S'ha de suposar que travessa la recta eL fins al punt L, desplaçat horitzontalment d'E per una petita distància, o, en lloc de l'arc eE. S'ha de tenir en compte que eL no és la tangent a e, i que o és negativa quan L està entre B i E. S'ha de traçar la línia que passa per E paral·lela a CH, tallant eL a n. A partir d'una propietat de la cicloide, En és la normal a la tangent a E, i de la mateixa manera la tangent a E és paral·lela a VH.

Com que el desplaçament, EL és petit, difereix poc en direcció de la tangent a E, de manera que l'angle EnL és proper a un angle recte. En el límit a mesura que l'arc eE s'acosta a zero, eL esdevé paral·lel a VH, sempre que o sigui petit en comparació amb eE fent que els triangles EnL i CHV siguin semblants.

També s'acosta a la longitud de la corda eE, i l'augment de la longitud, $eL-eE=nL={\frac {o.CH}{CV}}$, ignorant els termes en $o^{2}$ i superior, que representen l'error degut a l'aproximació que eL i VH són paral·lels.

La velocitat al llarg de eE o eL es pot prendre com la de E, proporcional a ${\sqrt {CB}}$, que és com CH, a partir de $CH={\sqrt {CB.CV}}$

Això sembla ser tot el que conté la nota de Gregory.

Sigui t el temps addicional per arribar a L,

$t\propto {\frac {nL}{\sqrt {CB}}}={\frac {o.CH}{CV.{\sqrt {CB}}}}={\frac {o}{\sqrt {CV}}}$

Per tant, l'augment del temps per travessar un petit arc desplaçat en un punt final depèn només del desplaçament al punt final i és independent de la posició de l'arc. Tanmateix, segons el mètode de Newton, aquesta és només la condició necessària perquè la corba es travessa en el mínim temps possible. Per tant, conclou que la corba mínima ha de ser la cicloide.

Ell argumenta el següent:

Suposant ara que la figura 1 és la corba mínima encara no determinada, amb l'eix vertical CV, i el cercle CHV eliminat, i la figura 2 mostra part de la corba entre l'arc infinitesimal eE i un arc infinitesimal més Ff a una distància finita al llarg del corba. El temps addicional, t, per recórrer eL (en lloc de eE) és nL dividit per la velocitat a E (proporcional a ${\sqrt {CB}}$), ignorant els termes en $o^{2}$ i superiors:

$t\propto {\frac {o.DE}{eE.{\sqrt {CB}}}}$,

A L, la partícula continua per un camí LM, paral·lel a l'EF original, fins a algun punt arbitrari M. Com que té la mateixa velocitat a L que a E, el temps per travessar LM és el mateix que hauria estat al llarg de la corba original EF. A M torna al camí original al punt f. Pel mateix raonament, la reducció de temps, T, per arribar a f des de M més que des de F és

$T\propto {\frac {o.FG}{Ff.{\sqrt {CI}}}}$

La diferència (t - T) és el temps addicional que triga al camí eLMf en comparació amb l'eEFf original :

$(t-T)\propto \left({\frac {DE}{eE{\sqrt {CB}}}}-{\frac {FG}{Ff{\sqrt {CI}}}}\right).o$ més termes en $o^{2}$ i superior (1)

Com que eEFf és la corba mínima, (t – T) is ha de ser major que zero, tant si o és positiva com negativa. Es dedueix que el coeficient de o a

(1) ha de ser zero:

${\frac {DE}{eE{\sqrt {CB}}}}={\frac {FG}{Ff{\sqrt {CI}}}}$

(2) en el límit quan eE i fF s'apropen a zero.

S'ha de tenir en compte que com que eEFf és la corba mínima, s'ha de suposar que el coeficient de $o^{2}$ és superior a zero.

És evident que hi ha d'haver dos desplaçaments iguals i oposats, o el cos no tornaria al punt final, A, de la corba.

Si e és fix, i si f es considera un punt variable més amunt de la corba, llavors per a tots aquests punts, f, ${\frac {FG}{Ff{\sqrt {CI}}}}$ és constant (igual a ${\frac {DE}{eE{\sqrt {CB}}}}$). En mantenir f fixa i fent e variable, queda clar que ${\frac {DE}{eE{\sqrt {CB}}}}$ també és constant.

Però, com que els punts, e i f són arbitraris, l'equació (2) només pot ser certa si ${\frac {DE}{eE{\sqrt {CB}}}}={\text{constant}}$, sempre, i aquesta condició caracteritza la corba que es busca. Aquesta és la mateixa tècnica que utilitza per trobar la forma del sòlid de menor resistència.

Per a la cicloide, ${\frac {DE}{eE}}={\frac {BH}{VH}}={\frac {CH}{CV}}$ , de manera que ${\frac {DE}{eE{\sqrt {CB}}}}={\frac {CH}{CV.{\sqrt {CB}}}}$, que es va mostrar més amunt com a constant, i la braquistòcrona és la cicloide.

Newton no dóna cap indicació de com va descobrir que la cicloide complia aquesta darrera relació. Pot haver estat per assaig i error, o pot haver reconegut immediatament que implicava que la corba era la cicloide.

Bibliografia

• Babb, Jeff; Currie, James «The Brachistochrone Problem: Mathematics for a Broad Audience via a Large Context Problem» ( PDF) (en anglès). The Montana Mathematics Enthusiast, 5(2), 5(3), juliol 2008. Arxivat de l'original el 2011-07-27 [Consulta: 22 novembre 2024].
• Bernoulli, Johann «Problema novum ad cujus solutionem Mathematici invitantur" (A new problem to whose solution mathematicians are invited)» (en llatí). Acta Eruditorum, 18, juny 1696.
• Bernoulli, Johann. Mémoires de l'Académie des Sciences (en francès). 3. Acadèmia Francesa de les Ciencies, 1718. 
• Costabel, Pierre; Peiffer, Jeanne. Der Briefwechsel von Johann I Bernoulli (en alemany). Vol. II: Der Briefwechsel mit Pierre Varignon, Erster Teil: 1692-1702. Springer Basel Aktiengesellschaft, 1988. ISBN 978-3-0348-5068-1. 
• Dubois, Jacques «Chute d'une bille le long d'une gouttière cycloïdale; Tautochrone et brachistochrone; Propriétés et historique» ( PDF) (en francès). Bulletin de l'Union des Physiciens, 85(737), 1991.
• Erlichson, Herman «Johann Bernoulli's brachistochrone solution using Fermat's principle of least time» (en anglès). Eur. J. Phys., 20(5), 1999. DOI: 10.1088/0143-0807/20/5/301.
• Freguglia, P.; Giaquinta, M. The Early Period of the Calculus of Variations (en anglès), 2016. ISBN 978-3-319-38945-5. 
• Galilei, Galileo. «Third Day, Theorem 22, Prop. 36». A: Discourses regarding two new sciences, 1638.  Aquesta conclusió havia aparegut sis anys abans al Diàleg sobre els dos sistemes mundials principals de Galileu (dia 4)
• Galilei, Galileo. Dialogue Concerning the Two Chief World Systems. Ptolemaic and Copernican translated by Stillman Drake, foreword by Albert Einstein (en anglès). University of California Press Berkeley; Los Angeles, 1967. 
• Hand, Louis N.; Janet, D. «cap. 2: Variational Calculus and Its Application to Mechanics». A: Analytical Mechanics (en anglès). Cambridge: Cambridge University Press, 1998. 
• Katz, Victor J. A History of Mathematics: An Introduction (en anglès). Addison Wesley Longman, 1998. ISBN 978-0-321-01618-8. 
• Livio, Mario. The Golden Ratio: The Story of Phi, the World's Most Astonishing Number (en anglès). Ciutat de Nova York: Broadway Books, 2003. 
• Ross, I. «The Brachistochrone Paradigm». A: Primer on Pontryagin's Principle in Optimal Control (en anglès). Collegiate Publishers, 2009. ISBN 978-0-9843571-0-9. 
• Sagan, Carl. Cosmos (en anglès). Random House Publishing Group, 2011. ISBN 9780307800985. 
• Stewart, James. «Section 10.1 - Curves Defined by Parametric Equations». A: Calculus: Early Transcendentals (en anglès). Belmont, CA: Thomson Brooks/Cole, 2012. 
• Struik, J. D.. A Source Book in Mathematics, 1200-1800 (en anglès). Harvard University Press, 1969. 
• Whiteside, Derek Thomas. The Mathematical Papers of Isaac Newton (en anglès). 8. Cambridge University Press, 2008. ISBN 978-0-521-20103-2. 

Enllaços externs

• Trott, Michael. «Brachistochrones» (en anglès). Wolfram Demonstrations Project.
• Arik, Okay. «Brachistochrone Problem» (en anglès). Wolfram Demonstrations Project.
• «Geodesics Revisited» ( PDF) (en anglès).«Brachistochrone problem in Python» (en anglès). Optimal control solution.