Anàlisi real
L'anàlisi real o teoria de les funcions de variable real és la branca de l'anàlisi matemàtica que s'ocupa dels nombres reals i les seves funcions, seqüències i sèries.[1] Es pot veure com una extensió rigorosa del càlcul, que estudia més profundament les successions de funcions i els seus límits, continuïtat, convergència, derivació i integració.
L'anàlisi real es distingeix de l'anàlisi complexa, que s'ocupa de l'estudi dels nombres complexos i les seves funcions.
Abast modifica
Construcció de nombres reals modifica
Els teoremes de l'anàlisi real es basen íntimament en l'estructura de la recta numèrica real. Aquesta consisteix en un conjunt no numerable ( ), juntament amb dues operacions binàries denotades + i ⋅, i un ordre denotat <, formant un cos. El sistema de nombres reals és l'únic cos ordenat complet (sense forats), és a dir, tot cos ordenat complet és isomorf a aquest. Els enfocaments moderns per definir nombres reals consisteixen a proporcionar una llista d'axiomes i una demostració de l'existència d'un model per a aquests, amb les propietats ja comentades.
Propietats d'ordre dels nombres reals modifica
Els nombres reals tenen vàries propietats relacionades amb la teoria de reticles i que són absents en nombres complexes. A més, formen un cos ordenat amb ordenació total, al qual les sumes i productes de nombres positius tenen com a resultat nombres positius.
Els nombres reals també tenen la propietat de que cada subconjunt de amb límit superior té un element suprem i ínfim que actua de límit superior inferior al primer i que també és real. Aquesta propietat condueix a una sèrie de resultats fonamentals en anàlisis reals, com el teorema monòton de convergència, el teorema del valor intermedi i el teorema del valor mitjà.
No obstant això, si bé els resultats de l'anàlisi real es defineixen per a nombres reals, molts d'aquests es poden generalitzar a altres objectes matemàtics. En particular, moltes idees d'anàlisi funcional i teoria dels operadors generalitzen propietats dels nombres reals.
Propietats topològiques dels nombres reals modifica
Molts dels teoremes d'anàlisi real són conseqüències de les propietats topològiques de la recta numèrica real, estretament relacionades amb les propietats d'ordre. Com a espai topològic, els nombres reals tenen una topologia estàndard, corresponent a la topologia d'ordre induïda per l'ordre . A més, si es defineix la funció de distància emprant la funció de valors absoluts , els nombres reals esdevenen l'exemple prototípic d'un espai mètric. La topologia induïda per resulta idèntica a la induïda per l'ordre . Degut a aquesta dualitat, alguns teoremes essencialment topològics per naturalesa com el teorema del valor intermedi es poden demostrar en espais topològics, no només en .
Seqüències modifica
Una seqüència és una funció que té com a domini un cos totalment ordenat i comptable. Aquest domini normalment són els nombres naturals,[2] tot i que en alguns casos és convenient considerar seqüències bidireccionals indexades pel conjunt de tots els enters, inclosos els índexs negatius.
Una seqüència és convergent quan tendeix a un límit, i divergent quan no. S'anomena acotada si existeix al qual per tots els . Finalment, es diu que una seqüència augmenta monotònicament si el valor de cada índex és igual o superior que l'anterior (i disminueix monotònicament si és igual o inferior), i per tant se l'anomena una seqüència monòtona. Aquesta propietat és estricta quan no té repeticions, és a dir quan es compleix tot i substituir o per < o >.
Donada una seqüència , una altra seqüència és una sub-seqüència de si per tots els enters positius i és una seqüència monòtona amb increment estricte de nombres naturals.
Límits i convergència modifica
El límit és el valor al qual una funció tendeix a mesura que l'índex s'aproxima a un valor, el qual pot incloure .[3] Aquesta idea és important en anàlisi matemàtica i la seva definició formal s'utilitza al seu torn per definir nocions com continuïtat, derivades i integrals.
En un context lleugerament diferent però relacionat, el concepte de límit s'aplica al comportament d'una seqüència a mesura que n incrementa.
La seqüència convergeix a si per tot valor té com a límit un nombre natural tal que implica que . Aquesta definició es pot generalitzar per tota funció substituint els nombres naturals i per nombres reals i ; en aquest cas implica que tendeix a , denotat , mentre que dona la corresponent definició del límit quan tendeix a , és a dir .
A vegades és útil concloure que una seqüència convergeix tot i que el valor al qual convergeix és desconegut o irrellevant. En aquests casos, el concepte de seqüència de Cauchy és útil. Diem que una seqüència és una seqüència de Cauchy si per tot hi ha un nombre natural tal que implica que .
A més de seqüències numèriques també existeixen seqüències de funcions en , és a dir, infinites famílies ordenades de funcions , denotades , amb propietats de convergència. En aquest cas hi ha dos tipus de convergència; puntual i uniforme.
- La convergència puntual de funcions a una funció limitant , denotada , significa que donada qualsevol , quan .
- La convergència uniforme de funcions , sovint denotada , implica que un valor ha d'existir per qualsevol , sense importar lo petita que sigui .
La uniforme és més robusta; tota seqüència amb convergència uniforme també té convergència puntual. Degut a això, per tal que l'intercanvi tingui un bon comportament, molts teoremes d'anàlisi real requereixen una convergència uniforme.
Compacitat modifica
La compacitat és un concepte de topologia general que té un paper important en molts dels teoremes de l'anàlisi real. La propietat de compacitat és una generalització de la noció d'un conjunt que és alhora tancat i fitat.
- Un conjunt és tancat si conté tots els seus punts límit.
- Un conjunt és fitat si existeix un nombre real tal que la distància entre dos punts del conjunt sigui menor que aquest nombre
En hi ha molts conjunts compactes incloent el conjunt buit, qualsevol nombre finit de punts, intervals tancats, i les seves unions finites.
Els conjunts compactes tenen un bon comportament respecte a propietats com la convergència i la continuïtat. Per exemple, qualsevol seqüència de Cauchy en un espai mètric compacte és convergent. La imatge d'un espai mètric compacte sota un mapa continu també és compacta.
Continuïtat modifica
Una funció des del conjunt de nombres reals fins als nombres reals es pot representar mitjançant una gràfica en el pla cartesià. A grans trets, aquesta funció és contínua si la gràfica està formada d'una única corba, sense "forats" ni "salts".
Hi ha vàries maneres de definir la continuïtat matemàticament, i s'utilitzarà la que millor s'adapti a una determinada situació.
- Si és un interval no degenerat, diem que és contínua a si ; diem que és un mapa continu si és contínua a cada . Perquè es pugui considerar contínua a , la funció ha d'estar definida en aquest punt (és a dir, el punt ha de formar part del domini de la funció) i quan . Aquesta definició s'aplica a qualsevol domini que no contingui un punt aïllat, és a dir, quan cada és un punt límit de .
- Si és un sub-conjunt arbitrari de , diem que és contínua a si per cada existeix el qüal per tot , implica que . En aquest cas és un mapa continu si és contínua a cada . Una conseqüència d'aquesta definició és que és trivialment contínua en qualsevol punt aïllat , per tant la definició és consistent amb la definició més general de continuïtat per mapes entre espais topològics (incloent espais mètrics) i .
- La definició més general estipula que si i són espais topològics, és contínua a si és un veïnat de en per cada veïnat de en . Diem que és un mapa continu si és oberta en per cada oberta en .
La continuïtat d'una funció pot ser uniforme o absoluta.
Diferenciació modifica
La noció de la derivada d'una funció o diferenciabilitat s'origina en el concepte d'aproximar una funció a prop d'un punt determinat mitjançant la "millor" aproximació lineal. Aquesta aproximació, si existeix, és única i ve donada per la línia que és tangent a la funció en el punt donat , i el pendent de la línia és la derivada de la funció a .
Una funció és deferenciable a quan
existeix. Aquest límit s'anomena la derivada de a . La funció és la funció derivada de , possiblement només definida en un subgrup de .
Com a simple conseqüència de la definició, és contínua a si és diferenciable allà. Ara bé, la diferenciabilitat és una condició més forta que la continuïtat; una funció contínua pot tenir punts no diferenciables (veure la funció de Weierstrass). També és possible l'existència de derivades d'ordre superior, trobant la derivada d'una funció derivada, i així successivament.
Es poden classificar les funcions per la seva classe de diferenciabilitat. La classe consisteix en totes les funcions contínues. La classe consisteix en totes les funcions diferenciables a les quals la derivada és contínua, anomenades funcions contínuament diferenciables. En general, es pot definir recursivament una classe declarant com a conjunt de totes les funcions contínues i per tots els enters com a conjunt de totes les funcions diferenciables la derivada de les quals tingui classe .
Una funció infinitament diferenciable és una funció de classe , i totes les funcions analítiques ( ) formen part d'aquest tipus.
Sèries modifica
Una sèrie formalitza la noció imprecisa de prendre la suma d'una seqüència infinita de nombres. Aquesta idea d'obtenir un resultat finit com a resultat de la suma d'infinits nombres era contraintuïtiva a l'antiga Grècia i va conduir a formular nombroses paradoxes, per exemple les paradoxes de Zenó. Per això, la noció moderna ho defineix com una suma finita de termes de la seqüència, és a dir, una suma parcial, i s'hi aplica el concepte de límit quan tendeix a infinit, essent aquest límit el valor resultant.
Donada una seqüència , el conjunt de sumes parcials de la sèrie és . La sèrie és convergent si la seqüència obtinguda d'aquest conjunt de sumes parcials convergeix, i divergent si no. La "suma" d'una sèrie convergent és definida com el valor . Cal tenir en compte doncs que el terme "suma" en aquest cas es fa servir de manera figurativa per referir-se al límit de la seqüència de sumes parcials. Per exemple, a diferència del comportament de les sumes finites, reordenar els termes d'una sèrie infinita pot convergir a un resultat diferent, tal com succeeix al Teorema de reordenació de Riemann. Una seqüència té convergència absoluta si és convergent. Si tot i ser convergent no té aquesta propietat llavors té convergència condicional, o no absoluta.
- La sèrie geomètrica convergeix a 1.
- La sèrie harmònica és divergent ja que la seqüència de sumes parcials creix sense límit.
Sèries de Taylor modifica
La sèrie de Taylor d'una funció ƒ(x) de valor real o complex que és infinitament diferenciable en un nombre real o complex a és la sèrie de potència
la qual pot ser reescrita utilitzant notació sigma com
on n! denota el factorial de n i ƒ (n)(a) denota la n-derivada de ƒ evaluada al punt a. La derivada d'ordre 0 és ƒ, i (x − a)0 i 0! són 1. Quan a = 0 la sèrie s'anomena una sèrie de Maclaurin.
Una sèrie de Taylor de f al punt a pot divergir, convergir només al punt a, convergir per tots els punts x als quals (el més gran dels quals s'anomena radi de convergència), o convergir a tota la línia real. Una sèrie de Taylor fins i tot pot convergir a un valor diferent al valor de convergència d'aquell punt. Si la sèrie en un punt té un radi de convergéncia major de 0 llavors és analítica. Una funció analítica d'una variable real s'estén naturalment a una funció d'una variable complexa; d'aquesta manera la funció exponencial, el logaritme, les funcions trogonomètriques i les seves inverses es poden estendre a funcions d'una variable complexa.
Sèries de Fourier modifica
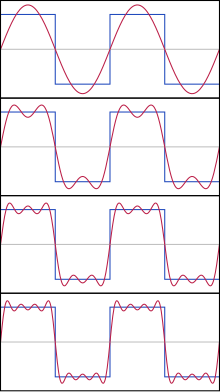
Les sèries de Fourier descomponen funcions periòdiques a la suma d'un conjunt (possiblement infinit) de funcions oscil·lants, és a dir, sinus i cosinus (o exponencials complexes).
Integració modifica
La integració és una formalització del problema de trobar l'àrea del pla comprès entre una corba i l'eix horitzontal, així com problemes relacionats en determinar la longitud d'una corba o el volum tancat per una superfície. L'estratègia bàsica per resoldre problemes d'aquest tipus era coneguda pels antics grecs i xinesos, i es coneixia com el mètode d'exhaustió. En termes generals, l'àrea desitjada es limita per sobre i per sota, respectivament, circumscrivint i inscrivint aproximacions poligonals cada vegada més precises les àrees exactes de les quals es poden calcular. En considerar aproximacions que consisteixen en un nombre cada vegada més gran de peces més petites es pot deduir l'àrea limitada per la corba, ja que els límits superior i inferior definits per les aproximacions convergeixen al voltant d'un valor comú.
Partint d'aquesta idea, una integral de Riemann es defineix en termes de sumes de funcions de Riemann respecte a les particions etiquetades d'un interval, les quals convergeixen a un valor comú quan són considerades les àrees de columnes rectangulars cada vegada més estretes. Quan les etiquetes escollides donen el valor màxim (i mínim, respectivament) de cada interval, la suma de Riemann es coneix com la suma superior (o inferior) de Darboux. Una funció és Darboux-integrable si es pot fer que les sumes de Darboux superior i inferior siguin arbitràriament properes entre si. Tot i que pot semblar un cas particular de la integral de Riemann, en realitat són definicions equivalents, és a dir, una integral és Darboux-integrable si i només si és Riemann-integrable.
Aquesta idea d'integral es pot extendir a una classe més àmplia de funcions, per així ampliar els dominis sobre els quals es poden definir aquestes funcions. Aquesta idea generalitzada d'integral s'anomena integral de Lebesgue.
El teorema fonamental del càlcul estipula que la derivada i integral d'una funció matemàtica són operacions inverses.
Distribucions modifica
Les distribucions, també anomenades funcions generalitzades, són objectes que generalitzen les funcions, és a dir, permeten derivar funcions les derivades de les quals no existeixen en el sentit clàssic. En particular, qualsevol funció localment integrable té una derivada distributiva.
Teoremes importants modifica
L'anàlisi real té tota una sèrie de teoremes de gran importància dins del camp de l'anàlisi matemàtica, com el teorema de Bolzano-Weierstrass, el teorema de Heine-Borel, el teorema del valor intermedi i el del valor mitjà, el teorema de Taylor, el teorema fonamental del càlcul, el teorema d'Arzelà-Ascoli, el teorema d'Stone-Weierstrass, el lema de Fatou i els teoremes de convergència monòtona i convergència dominada.
Relació amb l'anàlisi complexa modifica
L'anàlisi real està estretament relacionada amb l'anàlisi complexa, la qual estudia les mateixes propietats però en nombres complexos. En anàlisi complexa és natural definir la diferenciació mitjançant funcions holomorfes, que tenen una sèrie de propietats útils com que es poden derivar repetidament, es poden expressar com a sèrie de potències i satisfan la fórmula de la integral de Cauchy.
Alguns resultats com el teorema fonamental de l'àlgebra són més simples expressats en termes de nombres complexos. Ara bé, tècniques de la teoria de les funcions analítiques de variables complexes sovint s'utilitzen també en anàlisi real, com per exemple l'avaluació d'integrals reals mitjançant càlcul de residus.
Generalitzacions i àrees relacionades de les matemàtiques modifica
Es poden generalitzar diverses idees d'anàlisi real des de la línia real fins a contextos més amplis o abstractes. Aquestes generalitzacions relacionen l'anàlisi real amb altres disciplines. Per exemple, la generalització d'idees com funcions contínues i compacitat es poden utilitzar en espais mètrics i espais topològics dins del camp de la topologia general. La generalització dels espais euclidians de dimensions finites a anàlegs de dimensions infinites va conduir als conceptes d'espais de Banach i espais de Hilbert i, més generalment, a l'anàlisi funcional. La investigació de Georg Cantor sobre conjunts i seqüències de nombres reals, mapes entre ells i les qüestions fonamentals de l'anàlisi real van donar lloc a la teoria informal de conjunts. L'estudi de qüestions de convergència per a seqüències de funcions va donar lloc a l'anàlisi de Fourier com a subdisciplina de l'anàlisi matemàtica. La investigació de les conseqüències de la generalització de la diferenciabilitat de les funcions d'una variable real a les d'una variable complexa va donar lloc al concepte de funcions holomorfes i al començament de l'anàlisi complexa com una altra subdisciplina d'anàlisi diferent. D'altra banda, la generalització de la integració del sentit de Riemann al de Lebesgue va conduir a la formulació del concepte d'espais de mesura abstractes, un concepte fonamental en la teoria de la mesura. Finalment, la generalització de la integració de la línia real a les corbes i superfícies en un espai de dimensions superiors va suposar l'inici del càlcul vectorial, la posterior generalització i formalització del qual va tenir un paper important en l'evolució dels conceptes de formes diferencials i varietats diferenciables en geometria diferencial i altres àrees de geometria i topologia estretament relacionades.
Referències modifica
- ↑ Tao, Terence. «Lecture notes form MATH 131AH». Course Website for MATH 131AH. Department of Mathematics, UCLA, 2003.
- ↑ Gaughan, Edward. «1.1 Sequences and Convergence». A: AMS. Introduction to Analysis, 2009. ISBN 978-0-8218-4787-9.
- ↑ James, Stewart. Calculus: Early Transcendentals. 6. Brooks/Cole, 2008. ISBN 978-0-495-01166-8.
Vegeu també modifica
Bibliografia modifica
- Stephen, Abott. Springer-Verlag. Understanding Analysis. Nova York: Undergraduate Texts in Mathematics, 2001. ISBN 0-387-95060-5.
- Aliprantis, C. D.; Burkinshaw, O. Academic. Principles of real analysis. 3rd, 1998. ISBN 0-12-050257-7.
- Bartle, Robert G.; Sherbert, Donald R. John Wiley and Sons. Introduction to Real Analysis. 4th, 2011. ISBN 978-0-471-43331-6.
- Bressoud, David. A Radical Approach to Real Analysis. MMA, 2007. ISBN 978-0-88385-747-2.
- Browder, Andrew. «Undergraduate Texts in Mathematics». A: Springer-Verlag. Mathematical Analysis: An Introduction, 1996. ISBN 0-387-94614-4.
- Carothers, Neal L. Real Analysis. Cambridge: Cambridge University Press, 2000. ISBN 978-0521497565.
- Dangello, Frank; Seyfried, Michael. Introductory Real Analysis. Brooks Cole, 1999. ISBN 978-0-395-95933-6.
- Kolmogorov, A. N.; Fomin, S. V.. Introductory Real Analysis. Translated by Richard A. Silverman. Dover Publications, 1975. ISBN 0486612260.
- Rudin, Walter. «Walter Rudin Student Series in Advanced Mathematics». A: Principles of Mathematical Analysis. 3rd. Nova York: McGraw-Hill, 1976. ISBN 978-0-07-054235-8.
- Rudin, Walter. Real and Complex Analysis. 3rd. Nova York: McGraw-Hill, 1987. ISBN 978-0-07-054234-1.
- Spivak, Michael. Calculus. 3rd. Houston, Texas: Publish or Perish, Inc., 1994. ISBN 091409890X.
Enllaços externs modifica
- Weisstein, Eric W., «Real analysis» a MathWorld (en anglès). (anglès)
- Trench, William F. Introduction to Real Analysis. Prentice Hall, 2003. ISBN 978-0-13-045786-8.